Решение задачи 14
Рассмотрим однородное уравнение
Частное решение неоднородного уравнения будем искать в виде Имеем Подставим эти значения в неоднородное уравнение
Итак, Найдём частное решение:
Итак, найдём частное решение Ответ:
6. Выполнение и оформление контрольной работы Контрольная работа состоит из 10 вариантов, по 14 заданий в каждом, варианты выбираются студентом по последней цифре номера зачетной книжки. При выполнении работы студенты знакомятся с рекомендуемой основной и дополнительной литературой, с электронными ресурсами образовательного сайта ВСЭИ. Структура контрольной работы: с новой страницы – номер и содержание задания, ниже полное решение задачи, необходимые пояснения, чертежи, список литературы (введение, приложения не требуются). Оформление контрольной работы должно соответствовать требованиям, предъявляемым к выполнению контрольных работ во ВСЭИ.
7. Учебно-методическое обеспечение
А. Основная литература 1. Бортаковский А.С., Пантелеев А.В. Линейная алгебра в примерах и задачах. – М.: Высшая школа, 2005. 2. Высшая математика / Под ред. Н.Ш. Кремера. – М.: Высшее образование, 2006. 3. Линьков В.М.Высшая математика в примерах и задачах. Компьютерный практикум: учеб. пособие / В.М. Линьков, Н.Н. Яремко. – М.: ФиС, 2006.
Б. Дополнительная литература 1. Баврин И.И. Высшая математика. – М.: Академия, 2002. 2. Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра с элементами аналитической геометрии. – М.: Изд-во ВШЭ, 2007. 3. Бутузов и др. Математический анализ в вопросах и задачах: учеб. пособие для вузов. – М.: Высшая 4. школа, 1984. 5. Виленкин И.Я., Куницына Е.С., Мордкович А.Г. Математический анализ. Интегральное исчисление. - М.: Просвещение, 1979. 6. Власов В.Г. Конспект лекций по высшей математике. – М.: Айрис, 1996. 7. Гельфанд И.М. Лекции по линейной алгебре. – М.: Добросвет, 2006. 8. Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в упражнениях и задачах. Ч.1 и 2. – М.: Высшая школа. – 2009. 9. Зайцев И.А. Высшая математика. - М.: Высшая школа, 1998. 10. Левин М.Н., Рапопорт А.Н., Рапопорт Л.Д. Сборник задач по математике для экономистов. - Киров, 1998. 11. Лунгу К.Н. Сборник задач по высшей математике. - М.: Айрис – Пресс, 2006. 12. Малугин В.А. Математика для экономистов: Математический анализ. Курс лекций. - М.: Эксмо, 2006. 13. Малугин В.А. Математика для экономистов: Математический анализ. Задачи и упражнения. - М.: Эксмо, 2006. 14. Мироненко Е.С. Высшая математика: Методические указания и контрольные задания. - М.: Высшая школа, 2000. 15. Рапопорт А.Н. Высшая математика. Образовательный курс. - Киров, 2000. 16. Самаров К.Л., Шапкин А.С. Задачи с решениями по высшей математике и математическим методам в экономике: учебное пособие. - М.: «Дашков и Ко», 2007. 17. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - М.: Наука, 2004. 18. Шипачев В.С. Задачник по высшей математике. - М.: Высшая школа, 2004.
В. Электронные учебные материалы
1. Глушкова А.И., Зеленина Н.А., Шутова Б.И. Алгебра и геометрия [Электронный ресурс]: учебное пособие. – Киров: ВСЭИ, 2009. 2. Глушкова А.И., Зеленина Н.А. Математика [Электронный ресурс]: учебное пособие. – Киров: ВСЭИ, 2010. 3. Глушкова А.И. Математика [Электронный ресурс]: практикум. – Киров: ВСЭИ, 2011. 4. Зеленина Н.А. Математический анализ [Электронный ресурс]: учебное пособие. – Киров: ВСЭИ, 2010.
Г. Программное обеспечение Не предусмотрено.
Д. Базы данных, информационно-справочные и поисковые системы Не предусмотрено.
Глушкова Августа Игоревна
|

 ;
;  ,
,  .
.
 .
. . Соответствующее характеристическое уравнение имеет вид
. Соответствующее характеристическое уравнение имеет вид  ,
, . Следовательно,
. Следовательно,  - общее решение однородного уравнения.
- общее решение однородного уравнения. .
.
 .
.

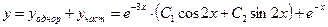 - общее решение.
- общее решение.

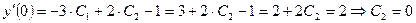 .
. .
. ;
;  .
.


