Физические основы эксперимента. - коэффициент Пуассона (показатель адиабаты) входит в уравнения, связывающие параметры газов (давление Р
По сути: Теплоемкостью вещества называется количество теплоты, необходимое для нагревания его на 1К:
Теплоемкость одного моля вещества называется молярной:
Теплоемкость единицы массы называется удельной:
Здесь Из двух последних формул следует, что Теплоемкость газов зависит от характера протекающих в них процессов. Согласно первому началу термодинамики, теплота
При постоянном объеме работа не совершается, поэтому теплота идет только на изменение внутренней энергии. При постоянном давлении требуется теплоты больше, чем при постоянном объёме, так как часть её идёт на совершение работы. Следовательно, теплоемкость при постоянном давлении Если произвести расчеты
где R= 8,31 Молярные теплоемкости могут быть выражены через число степеней свободы Тогда Для одноатомных газов (He, Ne, Ar): Для двухатомных газов (O2, N2, воздух): Для многоатомных газов(CO2, CH4, C2H2): Методика экспериментального определения Если теперь открыть кран К, то часть воздуха быстро выйдет из сосуда, то есть произойдет адиабатический процесс расширения, вследствие кратковременности протекания процесса и низкой теплопроводности стеклянного баллона теплота не успеет поступить в баллон, и работа расширения произойдет за счет уменьшения внутренней энергии. Поэтому температура воздуха понизится до Т. Параметры воздуха в конце адиабатического расширения, то есть в состоянии 2 будут равны: Если в момент установления атмосферного давления закрыть кран, то воздух будет нагреваться при постоянном объёме до комнатной температуры за счет поступления теплоты через стенки баллона, и давление будет повышаться. В конце этого процесса установится давление Отметим, что пунктирная кривая 1-3-3' является изотермой. Примечание. Нетрудно видеть, что в ходе эксперимента масса газа в баллоне меняется и всегда больше первоначальной массы
В состояниях 1 и 3 температура одинакова, поэтому из уравнения Менделеева-Клапейрона следует: Параметры состояний 1 и 2 связаны с уравнением Пуассона для адиабатического процесса:
Принимая во внимание, что
Однако на практике очень трудно совместить закрытие крана с моментом окончания адиабатического процесса. Если задержать закрытие крана на некоторое время, то воздух будет расширяться вследствие нагревания при постоянном атмосферном давлении (2 -2´на рис.2). Если спустя некоторое время кран закрыть, то воздух будет нагреваться при постоянном объеме до комнатной температуры (изохора (2-3') на рис.2). При этом значение избыточного давления меньше, чем
где Проведя опыт несколько раз с различными временами задержки t, и построив график
Рис.3. Зная Если время задержки t значительно больше времени адиабатического расширения, тогда его с достаточной точностью можно считать полным временем открытия крана.
|

 - коэффициент Пуассона (показатель адиабаты) входит в уравнения, связывающие параметры газов (давление Р, объём V, температуру Т) в адиабатическом процессе:
- коэффициент Пуассона (показатель адиабаты) входит в уравнения, связывающие параметры газов (давление Р, объём V, температуру Т) в адиабатическом процессе: (1),
(1),  (2),
(2), 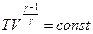 (3).
(3). , т.е. отношение теплоемкостей газа при постоянном давлении и объеме.
, т.е. отношение теплоемкостей газа при постоянном давлении и объеме. . (4)
. (4) . (5)
. (5) . (6)
. (6) - число молей,
- число молей,  - масса газа.
- масса газа. , где
, где  - молярная масса,
- молярная масса, 
 , сообщенная системе, идет на изменение внутренней энергии
, сообщенная системе, идет на изменение внутренней энергии  и на совершение работы
и на совершение работы  :
: (7)
(7) больше, чем теплоемкость при постоянном объеме
больше, чем теплоемкость при постоянном объеме  .
.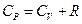 (8)
(8) - универсальная газовая постоянная.
- универсальная газовая постоянная. [ 1]:
[ 1]: 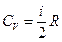 ,
,  .
. (9)
(9) будет сжата, то есть займет объём меньший объёма сосуда. Работа внешних сил приведёт к повышению давления и температуры в баллоне. В течение некоторого времени после окончания накачивания разность уровней жидкости будет уменьшаться, так как происходит понижения температуры и давления воздуха вследствие теплопроводности стенок баллона. Окончательная разность уровней жидкости в манометре
будет сжата, то есть займет объём меньший объёма сосуда. Работа внешних сил приведёт к повышению давления и температуры в баллоне. В течение некоторого времени после окончания накачивания разность уровней жидкости будет уменьшаться, так как происходит понижения температуры и давления воздуха вследствие теплопроводности стенок баллона. Окончательная разность уровней жидкости в манометре  установится, когда температура в баллоне станет равна комнатной. При этом газ массой
установится, когда температура в баллоне станет равна комнатной. При этом газ массой  , объём
, объём  и давление
и давление  (см. первую строку в таблице 1). На рис.2 это состояние газа обозначено цифрой 1.
(см. первую строку в таблице 1). На рис.2 это состояние газа обозначено цифрой 1. ,
,  ,
,  (вторая строка в таблице 1) График адиабатического расширения газа представлен на диаграмме (P-V) кривой 1-2.
(вторая строка в таблице 1) График адиабатического расширения газа представлен на диаграмме (P-V) кривой 1-2. , объём
, объём  , температура
, температура 



 Рис. 2.
Рис. 2. (10)
(10) (11)
(11) и
и 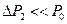 , решив систему уравнений (1) и 2) и заменив
, решив систему уравнений (1) и 2) и заменив  и
и  на разности высот уровней
на разности высот уровней 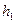 и
и  в манометре, получим формулу для расчета
в манометре, получим формулу для расчета  :
: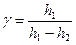 (12)
(12) меньше
меньше  , (13)
, (13) (рис. 3)
(рис. 3)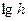 от t, можно экстраполяцией графика на t=0 найти
от t, можно экстраполяцией графика на t=0 найти  как точку пересечения графика с осью ординат (рис. 3). Тогда
как точку пересечения графика с осью ординат (рис. 3). Тогда  (14)
(14)



