Физические основы эксперимента
1. Ефимова М.Р., Петрова Е.В, Румянцев В,Н, Общая теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.: ИНРА-М, 2000. – 416с. 2. Назаров М.Г., Адамов В.Е., Беляевский и др. Курс социально-экономической статистики. Под ред. проф. М.Г. Назарова. Учебник. Изд. 2-е перераб. и доп. – М.: Финансы и статистика, 1985. – 607с. 3. Экономическая статистика. 2-е изд., доп.: Учебник/Под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 2000. – 480с. – (Серия «Высшее образование»). 4. Яблочник. А.Л. Общая теория статистики. Под ред. Проф. И.С. Пасхавера. Учеб. Пособие для студентов экон. специальностей вузов. М., «Статистика», 1976. – 344с.
Лабораторная работа №11 Изучение статистических закономерностей Цель работы: изучение характера распределения дроби в установке Гальтона и распределения термоэлектронов по модулям скоростей.
Эксперимент 1. Исследование распределения дроби в горизонтальной плоскости при прохождении её через систему решёток. Описание лабораторной установки и оборудования Эксперимент проводится на установке, (так называемая доска Гальтона), схема которой приведена на рис. 1
Рис. 1 Схема экспериментальной установки Она представляет собой плоскую вертикальную коробку с прозрачной передней стенкой. Через воронку в установку насыпают дробь, которая падая вниз через систему штырьков, попадает в ячейки. При соударении со штырьками происходит отклонение дробинок в горизонтальной плоскости, носящее случайный характер. С одной стороны коробки имеется 3 ряда штырьков, с другой – 12. На прозрачные стенки ячеек нанесены деления, по которым можно определить уровень заполнения ячеек дробью. Общие сведения Физические основы эксперимента
Все макроскопические тела состоят из огромного числа атомов и молекул, которые находятся в непрерывном хаотическом движении. В силу этого скорости, импульсы, энергии, координаты и т. д. отдельных молекул – величины случайные. Поэтому в совокупном поведении отдельных молекул появляются статистические закономерности. Их изучение и делает возможным описание макросистем на основе сведений о свойствах отдельных частиц системы. Математическим аппаратом статистической физики является теория вероятности Статистическая физика связывает макропараметры тел (давление, температура, плотность, теплопроводность, вязкость и т. п.) со средними значениями микропараметров молекул (скоростью, координатами, импульсом и др.). Последние могут быть вычислены с помощью так называемой функции распределения, смысл которой определяется выражением:
где x – какой-то микропараметр молекул, N – общее число молекул, dx- интервал числовых значений параметра х, Если математический вид функции распределения известен, то среднее значение микропараметра х в интервале от некоторого xmin до некоторого xmax может быть вычислено по формуле:
Может быть вычислено число молекул:
Поэтому отыскание математического вида функции распределения – одна из основных задач статистической физики.
Примером функции распределения является нормальное распределение или распределение Гаусса. Распределению Гаусса подчиняются случайные ошибки экспериментальных измерений (см. стр. 5-6 настоящего пособия); нормальным (гауссовским) является распределение молекул идеального газа по проекциям скоростей Vx на произвольную ось [1, 2, 3]:
где m – средняя масса молекул, k- постоянная Больцмана, Т- температура. Графики этой функции для двух температур Т1 и Т2 (Т2 ˃Т1) приведен на рис. 2.
  
Рис. 2. Графики функции распределения Гаусса.
Из графиков следует, что: 1. Число молекул, имеющих положительные проекции скорости (т.е движущиеся по оси х), равно числу молекул, имеющих отрицательные проекции скорости (т.е. движущихся против оси х), т.к. график в целом симметричен относительно вертикальной оси и площади под ним слева и справа от оси f(Vx) одинаковы. 2. Наиболее вероятное значение Vx, соответствующее максимуму функции распределения f(Vx), равно нулю. 3. При повышении температуры газа график f(Vx) оставаясь симметричным становится более пологим. Это говорит о том, что при нагревании газа уменьшается число молекул с малыми (близкими к нулю) проекциями скоростей, и увеличивается число молекул с большими проекциями скоростей. Очевидно это связано с тем, что при повышении температуры газа в целом увеличиваются скорости его молекул.
В данной работе в первом эксперименте исследуется распределение дроби в горизонтальном направлении после прохождения её через систему рассеивающих штырьков (см. рис. 1), которое при определённых условиях является распределением Гаусса. Поясним, почему это происходит. Выйдя из воронки, любая дробинка движется первоначально вертикально вниз. При ударе о штырьки дробинка случайным образом отклоняется от вертикали, приобретая какую-то скорость Vx в горизонтальном направлении, и попадает в некоторую ячейку. Чем больше Vx, тем в более удалённую от центра ячейку попадёт дробинка. Просыпав всю дробь через систему штырьков, можно получить гистограмму заполнения ячеек дробью (см.рис.3). Вероятность того, что наугад взятая дробинка попадёт в ячейку с координатой х, будет определяться по формуле:
где О виде функции распределения В свою очередь
Рис. 3 Распределение дроби по ячейкам.
В данном опыте отклонение дроби равновероятно в обе стороны от центра воронки. Это является характерной чертой распределения Гаусса. Однако при экспериментальном исследовании этого распределения возможно действие каких-либо факторов, которые нарушат симметрию и общий вид графиков. Симметричность экспериментальных графиков можно оценить расчетом среднего значения <x> по формуле:
Т. к. ∆Ni пропорционально высоте заполнения ячеек дробью Нi, то вместо (13) получим:
Наиболее вероятное значение хв определяется по максимуму графика функции распределения.
Примечание. По указанию преподавателя может быть проведена дополнительная проверка экспериментально полученных распределений дроби на соответствие их нормальному распределению Гаусса (расчетом среднеквадратичных отклонений и коэффициента асимметрии). Формулы для расчета можно найти в [4].
|


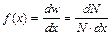 , (1)
, (1) - вероятность обнаружения молекул с параметром х из интервала dх.
- вероятность обнаружения молекул с параметром х из интервала dх. (2)
(2) (3)
(3) , (4)
, (4)








 , (5)
, (5) - число дробинок, попавших в данную ячейку,
- число дробинок, попавших в данную ячейку,  - общее число дробинок,
- общее число дробинок,  - ширина ячейки,
- ширина ячейки,  - функция распределения дробинок по ячейкам.
- функция распределения дробинок по ячейкам. можно будет судить по величине
можно будет судить по величине  -величины фиксированные.
-величины фиксированные. , описывающей распределение дроби по ячейкам (см. рис.3).
, описывающей распределение дроби по ячейкам (см. рис.3).
 . (6)
. (6) . (7)
. (7)


