Физические основы эксперимента. При течении воздуха в капилляре разные его слои движутся с разными скоростями
При течении воздуха в капилляре разные его слои движутся с разными скоростями. На рисунке 2 в плоскости максимального горизонтального сечения капилляра схематично показаны скорости отдельных слоев воздуха
Рис. 2. В результате хаотического теплового движения молекулы воздуха будут переходить из слоя в слой. При перемещении молекул из быстрого слоя в более медленный (например, из слоя Б в слой А на рис.2) будет переноситься б о льший импульс, чем в обратном направлении.В результате произойдет изменениеимпульсов слоев в направлении Х на величину
где Уравнение (1) позволяет найти силы, действующие на движущиеся слои газа. Т. к. по второму закону Ньютона
Это сила, которая тормозит быстро движущийся слой газа (на рис.2 – слой Б), и ускоряет медленно движущийся слой (на рис.2 –слой А). Это так называемая сила внутреннего трения, действие которой приводит к выравниванию скоростей отдельных слоев воздуха.
При ламинарном (без завихрений) течении воздуха по капилляру лабораторной установки устанавливается равенство между силой внутреннего трения и силой, обусловленной разностью давлений
где Из (3) следует, что
Т.к.
где Эта формула используется для экспериментального определения коэффициента вязкости в данной лабораторной работе. В заключении отметим, что теоретическое описание внутреннего трения [1,2], определяет коэффициент вязкости как
где
Здесь
|

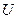 : минимальные скорости имеют слои, прилегающие к стенкам капилляра (из-за трения о стенку), наибольшие скорости имеют центральные слои воздушного потока.
: минимальные скорости имеют слои, прилегающие к стенкам капилляра (из-за трения о стенку), наибольшие скорости имеют центральные слои воздушного потока.
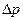 , пропорциональную градиенту скорости
, пропорциональную градиенту скорости  (т.е. изменению скорости на единицу длины в направлении Z): импульс быстрого слоя уменьшится, а медленного – увеличится на одну и ту же величину
(т.е. изменению скорости на единицу длины в направлении Z): импульс быстрого слоя уменьшится, а медленного – увеличится на одну и ту же величину  , (1)
, (1)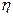 - коэффициент вязкости (или внутреннего трении),
- коэффициент вязкости (или внутреннего трении),  - площадь соприкосновения слоев,
- площадь соприкосновения слоев,  - время; знак «минус» показывает, что перенос импульса происходит в сторону слоев с меньшими скоростями
- время; знак «минус» показывает, что перенос импульса происходит в сторону слоев с меньшими скоростями  , то из (1) следует, что
, то из (1) следует, что . (2)
. (2) на концах капилляра. В этих условиях объем газа
на концах капилляра. В этих условиях объем газа  , прошедший через капилляр за время
, прошедший через капилляр за время  , определяется законом Пуазейля [1, §77]:
, определяется законом Пуазейля [1, §77]: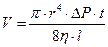 , (3)
, (3) - внутренний радиус капилляра,
- внутренний радиус капилляра, 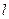 - его длина.
- его длина. . (4)
. (4)
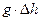 , где
, где  - плотность жидкости в манометре,
- плотность жидкости в манометре,  - разность уровней жидкости в манометре, то после подстановки этого выражения в (4) получим:
- разность уровней жидкости в манометре, то после подстановки этого выражения в (4) получим: , (5)
, (5)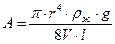 - совокупность постоянных для эксперимента величин.
- совокупность постоянных для эксперимента величин.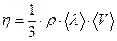 , (6)
, (6)
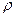 - плотность газа:
- плотность газа: 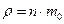 ,
, - средняя длина свободного пробега молекул:
- средняя длина свободного пробега молекул:  ,
, - средняя скорость молекул:
- средняя скорость молекул:  .
. - концентрация молекул,
- концентрация молекул,  -масса молекулы,
-масса молекулы,  -эффективный диаметр молекулы,
-эффективный диаметр молекулы,  - постоянная Больцмана,
- постоянная Больцмана,  - температура газа.
- температура газа.


