Решить задачу, используя теоремы Муавра – Лапласа.
1 Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
2 Вероятность наступления события в каждом из независимых испытаний равна 0,2. Проведено 900 испытаний. Найти вероятность того, что относительная частота появления события отклонится от его вероятности не более чем на 0,04.
3 Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится:
а) 1400 раз,
б) не менее 1470 и не более 1500 раз?
4 Вероятность изготовления изделия отличного качества равна 0,8. Найти вероятность того, что среди взятых 60 изделий 30 окажутся отличного качества.
5 Фабрика выпускает в среднем 70% изделий первого сорта. Найти вероятность того, что в партии из 1000 изделий число первосортных заключено между 652 и 760.
6 При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Определить вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
7 Штамповка металлических клемм для соединительных пластин дает 20% брака. Пользуясь теоремой Лапласа, определить вероятность наличия от 100 до 125 клемм, не соответствующих стандарту, в партии из 600 клемм.
8 Вероятность рождения мальчика 0,515. Какова вероятность того, что среди 1000 новорожденных будет 480 девочек?
9 Процент отсева среди студентов первокурсников составляет 10%. Найти вероятность того, что из 900 будет отчислено от 80 до 110 студентов (включительно).
10 Вероятность того, что покупателю необходима обувь 41-го размера равна 0,2. Найти вероятность того, что из 750 не более 120 потребуют такую обувь.
11 Объем продаж в течение месяца – это случайная величина, подчиненная нормальному закону распределения с параметрами 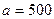 и и  . Найти вероятность того, что объем товара в данном месяце заключен в границах от 480 до 600. . Найти вероятность того, что объем товара в данном месяце заключен в границах от 480 до 600.
12 Вероятность того, что деталь не проверялась ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется от 70 до 100 деталей, не проверенных ОТК.
13 По статистическим данным, в 20% случаев коммерческому банку удается привлечь имеющихся у населения сбережения. Найти вероятность того, что среди населения данного округа численностью 1500 человек доля граждан, желающих вложить свои сбережения в коммерческий банк, отклонится от указанной вероятности не более чем на 0,03 (по абсолютной величине).
14 Было посажено 500 кустарников, вероятность прижиться каждому из которых равна 0,8. Оценить вероятность того, что приживутся от 100 до 440 кустарников (включительно).
15 Найти вероятность того, что среди наудачу взятых 100 деталей 55 окажутся отполированными, если в общей массе деталей имеется поровну отполированных и не отполированных.
5. Дана случайная величина. Требуется:
а) найти закон распределения случайной величины Х (для первых пяти заданий),
б) построить многоугольник распределения случайной величины Х,
в) найти её функцию распределения 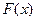 , ,
г) построить график 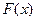 , ,
д) найти М(Х), D(X),  (X), если: (X), если:
1 Х – число выпадений герба при четырёх подбрасываниях монетки
2 Х – количество попаданий в мишень при трёх выстрелах, вероятность каждого попадания 0,7
3 Х – количество попаданий в мишень при трёх выстрелах, вероятность первого попадания 0,8, второго – 0,7, третьего – 0,4
4 Х – число выпадений пяти очков при трёх подбрасываниях игральной кости
5 Х – число дождливых дней в неделю, если количество дождливых дней в году 170.
| xi
| 0,5
| 1,0
| 1,7
| 2,0
| 2,4
| 2,8
| | pi
| 0,1
| 0,15
| 0,2
| 0,22
| 0,18
| 0,15
|
| xi
| 1,5
| 3,2
| 5,1
| 7,4
| 8,9
| 10,5
| | pi
| 0,05
| 0,09
| 0,15
| 0,21
| 0,29
| 0,21
|
| xi
|
|
|
|
|
|
|
| | pi
| 0,03
| 0,06
| 0,11
| 0,17
| 0,23
| 0,22
| 0,18
|
| xi
|
|
|
|
|
|
|
|
| | pi
| 0,02
| 0,08
| 0,14
| 0,17
| 0,19
| 0,16
| 0,13
| 0,11
|
| xi
| 10,1
| 10,8
| 11,6
| 12,5
| 13,6
| 14,8
| | pi
| 0,12
| 0,15
| 0,19
| 0,23
| 0,17
| 0,14
|
| xi
| 10,1
| 10,3
| 10,5
| 10,6
| 10,8
| | pi
| 0,1
| 0,2
| 0,3
| 0,2
| 0,2
|
| xi
| 0,5
| 1,5
| 2,6
| 3,8
| 4,3
| | pi
| 0,1
| 0,2
| 0,4
| 0,2
| 0,1
|
| xi
| -4,7
| -4,5
| -4,2
| -3,9
| -3,4
| | pi
| 0,11
| 0,13
| 0,22
| 0,24
| 0,3
|
| xi
|
|
|
|
|
|
| | pi
| 0,15
| 0,20
| 0,25
| 0,20
| 0,15
| 0,05
|
| xi
|
|
|
|
|
|
|
| | pi
| 0,12
| 0,13
| 0,18
| 0,20
| 0,15
| 0,17
| 0,05
| Тема №2 «Проверка статистических гипотез»
Из двух нормально распределенных генеральных совокупностей 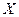 и и 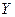 получены малые независимые выборки, объемы которых получены малые независимые выборки, объемы которых
 и и 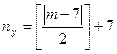 , ,
где [ ] означают целую часть числа, заключенного в эти скобки, 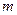 - порядковый номер фамилии студента в групповом журнале. - порядковый номер фамилии студента в групповом журнале.
Значения вариант 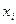 и и 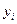 рассчитываются по формулам: рассчитываются по формулам:
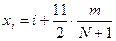 , , 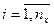 и и 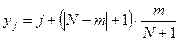 , , 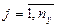 , ,
где 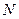 – номер студенческой группы. – номер студенческой группы.
Требуется по данным выборкам при уровне значимости 0,05 проверить нулевую гипотезу 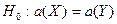 при альтернативной гипотезе при альтернативной гипотезе 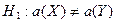 . .
Пример вычисления для студента с параметрами 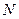 =0, =0, 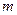 =1. =1.
Решение. Определим объемы выборок:
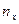 = = 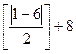 = = 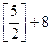 =[2,5]+8=2+8=10 =[2,5]+8=2+8=10
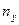 = = 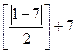 = = 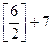 =[3]+7=3+7=10. =[3]+7=3+7=10.
Далее найдем значения вариант обеих выборок:
x1=1+5,5=6,5; x2=7,5; x3=8,5; x4=9,5; x5=10,5; x6=11,5; x7=12,5; x8=13,5; x9=14,5; x10=15,5;
y1= 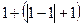 =2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11. =2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11.
Вычислим средние и исправленные дисперсии:
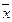 =11; =11;
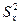 = = 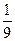 ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)= ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)= 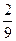 · 41,25= · 41,25= 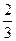 · 13,756≈9,167, · 13,756≈9,167,
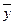 =6,5; =6,5;
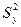 = = 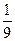 ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=9,167. ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=9,167.
Проверим сначала гипотезу о равенстве дисперсий 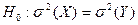 , при конкурирующей , при конкурирующей 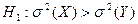 . .
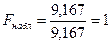 , , 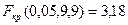 , так как , так как 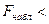 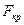 , то гипотеза о равенстве дисперсий принимается. , то гипотеза о равенстве дисперсий принимается.
Можно переходить к сравнению математических ожиданий.
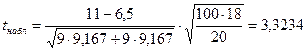 , , 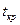 (0,05,18)=2,10, так как (0,05,18)=2,10, так как 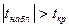 то гипотеза то гипотеза 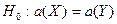 о равенстве математических ожиданий отвергается. о равенстве математических ожиданий отвергается.
Тема №3 «Оценивание параметров и проверка гипотезы о нормальном законе распределения»
По выборочным данным, представленным ниже, требуется проверить гипотезу о нормальном законе распределения по критериям согласия Пирсона и критерию Колмогорова на уровне значимости 0,05.
Здесь 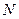 - номер студенческой группы, - номер студенческой группы, 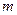 - номер фамилии студента в журнале. - номер фамилии студента в журнале.
| 11,70
| 12,90
| 10,32
| 9,50
| 5,91
| 11,56
| 10,81
| 9,32
| 13,00
| 12,90
| | 7,35
| 11,80
| 17,00+ 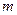 /10 /10
| 14,10
| 9,74
| 9,76
| 6,96
| 15,05
| 14,67
| 9,73+N/10
| | 11,35
| 10,51
| 15,95
| 12,41
| 13,56
| 6,68
| 13,75
| 16,95
| 8,81
| 10,60+N/10
| | 13,90
| 9,03
| 7,39
| 13,85
| 11,99
| 6,23
| 12,56
| 12,03
| 12,97
| 15,95
| | 11,00
| 7,76
| 10,48
| 12,80
| 12,05
| 12,33
| 5,60- 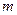 /10 /10
| 8,80
| 9,85
| 10,11+ 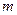 /10 /10
| | 9,75
| 13,70
| 12,09
| 13,40
| 9,02
| 6,67
| 12,37
| 11,67
| 12,00
| 13,60
| | 15,21
| 9,70
| 13,70
| 16,10
| 13,60
| 14,40
| 14,75
| 8,06
| 13,01
| 10,70+N/10
| | 13,57
| 15,30
| 12,30
| 15,85
| 17,60
| 11,25
| 12,75
| 11,50
| 12,27
| 11,50
| | 9,21
| 10,79
| 11,11
| 12,31
| 16,80
| 16,20
| 10,36
| 6,86
| 12,90
| 8,64+(N+ 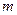 )/10 )/10
| | 14,90
| 16,00
| 12,00
| 12,31
| 9,35
| 16,60
| 15,67
| 15,33
| 8,69+ 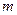 /10 /10
| 12,07
|
Пример вычисления для студента с параметрами 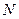 =0, =0, 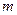 =0. =0.
Решение.
| 11,70
| 12,90
| 10,32
| 9,50
| 5,91
| 11,56
| 10,81
| 9,32
| 13,00
| 12,90
| | 7,35
| 11,80
| 17,00
| 14,10
| 9,74
| 9,76
| 6,96
| 15,05
| 14,67
| 9,73
| | 11,35
| 10,51
| 15,95
| 12,41
| 13,56
| 6,68
| 13,75
| 16,95
| 8,81
| 10,60
| | 13,90
| 9,03
| 7,39
| 13,85
| 11,99
| 6,23
| 12,56
| 12,03
| 12,97
| 15,95
| | 11,00
| 7,76
| 10,48
| 12,80
| 12,05
| 12,33
| 5,60
| 8,80
| 9,85
| 10,11
| | 9,75
| 13,70
| 12,09
| 13,40
| 9,02
| 6,67
| 12,37
| 11,67
| 12,00
| 13,60
| | 15,21
| 9,70
| 13,70
| 16,10
| 13,60
| 14,40
| 14,75
| 8,06
| 13,01
| 10,70
| | 13,57
| 15,30
| 12,30
| 15,85
| 17,60
| 11,25
| 12,75
| 11,50
| 12,27
| 11,50
| | 9,21
| 10,79
| 11,11
| 12,31
| 16,80
| 16,20
| 10,36
| 6,86
| 12,90
| 8,64
| | 14,90
| 16,00
| 12,00
| 12,31
| 9,35
| 16,60
| 15,67
| 15,33
| 8,69
| 12,07
| Для удобства расположим варианты в порядке возрастания.
| 5,60
| 8,06
| 9,50
| 10,48
| 11,50
| 12,05
| 12,56
| 13,56
| 14,40
| 15,95
| | 5,91
| 8,64
| 9,70
| 10,51
| 11,50
| 12,07
| 12,75
| 13,57
| 14,67
| 15,95
| | 6,23
| 8,69
| 9,73
| 10,60
| 11,56
| 12,09
| 12,80
| 13,60
| 14,75
| 16,00
| | 6,67
| 8,80
| 9,74
| 10,70
| 11,67
| 12,27
| 12,90
| 13,60
| 14,90
| 16,10
| | 6,68
| 8,81
| 9,75
| 10,79
| 11,70
| 12,30
| 12,90
| 13,70
| 15,05
| 16,20
| | 6,86
| 9,02
| 9,76
| 10,81
| 11,80
| 12,31
| 12,90
| 13,70
| 15,21
| 16,60
| | 6,96
| 9,03
| 9,85
| 11,00
| 11,99
| 12,31
| 12,97
| 13,75
| 15,30
| 16,80
| | 7,35
| 9,21
| 10,11
| 11,11
| 12,00
| 12,33
| 13,00
| 13,85
| 15,33
| 16,95
| | 7,39
| 9,32
| 10,32
| 11,25
| 12,00
| 12,37
| 13,01
| 13,90
| 15,67
| 17,00
| | 7,76
| 9,35
| 10,36
| 11,35
| 12,03
| 12,41
| 13,40
| 14,10
| 15,85
| 17,60
| 1) находим размах выборки:
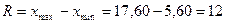 , ,
2) определяем число классов разбиения по формуле Стерджесса:
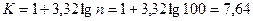 , ,
3) находим величину классового интервала:
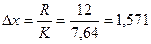 , ,
4) границы и середины частичных интервалов находим по формулам:
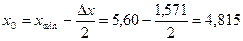 , ,
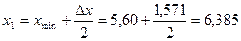 , ,
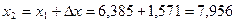 и так далее, и так далее,
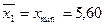 , ,
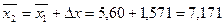 и так далее. и так далее.
5) подсчитываем частоты попадания вариант в каждый интервал:
| Границы
интервалов
| Середина
интервала
| Эмпирическая
частота
| 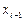
| 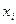
| 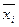
| 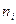
| | 4,815
| 6,385
| 5,600
|
| | 6,385
| 7,956
| 7,171
|
| | 7,956
| 9,527
| 8,741
|
| | 9,527
| 11,097
| 10,312
|
| | 11,097
| 12,668
| 11,883
|
| | 12,668
| 14,239
| 13,453
|
| | 14,239
| 15,809
| 15,024
|
| | 15,809
| 17,380
| 16,595
|
| | 17,380
| 18,951
| 18,165
|
|
Эмпирический интервальный ряд составлен, найдём среднее значение и СКО:
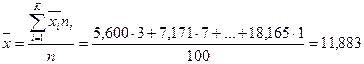 , , 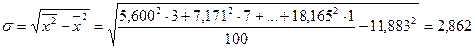 . .
Теперь найдём теоретические частоты, предполагая нормальное распределение совокупности:
| Границы
интервалов
|
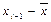
|
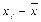
| Границы
интервалов
|
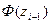
|
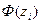
|
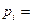 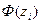 -
- -
- 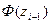
|
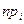
|
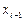
|
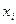
| 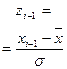
| 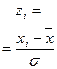
| | 4,815
| 6,385
| -
| -5,497
| 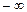
| -1,921
| -0,5
| -0,4726
| 0,0274
| 2,74
| | 6,385
| 7,956
| -5,497
| -3,927
| -1,921
| -1,372
| -0,4726
| -0,4147
| 0,0579
| 5,79
| | 7,956
| 9,527
| -3,927
| -2,356
| -1,372
| -0,823
| -0,4147
| -0,2939
| 0,1208
| 12,08
| | 9,527
| 11,097
| -2,356
| -0,785
| -0,823
| -0,274
| -0,2939
| -0,1064
| 0,1875
| 18,75
| | 11,097
| 12,668
| -0,785
| 0,785
| -0,274
| 0,274
| -0,1064
| 0,1064
| 0,2128
| 21,28
| | 12,668
| 14,239
| 0,785
| 2,356
| 0,274
| 0,823
| 0,1064
| 0,2939
| 0,1875
| 18,75
| | 14,239
| 15,809
| 2,356
| 3,923
| 0,823
| 1,372
| 0,2939
| 0,4147
| 0,1208
| 12,08
| | 15,809
| 17,380
| 3,923
| 5,497
| 1,372
| 1,921
| 0,4147
| 0,4726
| 0,0579
| 5,79
| | 17,380
| 18,951
| 5,497
| -
| 1,921
| 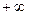
| 0,4726
| 0,5
| 0,0274
| 2,74
| 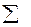
|
|
| Найдём наблюдаемые значения 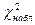 и и 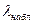 . .
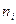
|
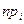
|
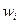
|
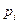
|
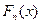
|
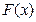
|
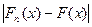
| 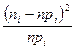
| |
| 2,74
| 0,03
| 0,0274
| 0,03
| 0,0274
| 0,0026
| 0,0247
| |
| 5,79
| 0,07
| 0,0579
| 0,10
| 0,0853
| 0,0147
| 0,2529
| |
| 12,08
| 0,11
| 0,1208
| 0,21
| 0,2061
| 0,0039
| 0,0966
| |
| 18,75
| 0,16
| 0,1875
| 0,37
| 0,3936
| 0,0236
| 0,4033
| |
| 21,28
| 0,24
| 0,2128
| 0,61
| 0,6064
| 0,0036
| 0,3477
| |
| 18,75
| 0,19
| 0,1875
| 0,80
| 0,7939
| 0,0061
| 0,0033
| |
| 12,08
| 0,09
| 0,1208
| 0,89
| 0,9147
| 0,0247
| 0,7853
| |
| 5,79
| 0,10
| 0,0579
| 0,99
| 0,9726
| 0,0174
| 3,0612
| |
| 2,74
| 0,01
| 0,0274
| 1,00
| 1,00
|
| 1,1050
| |
| 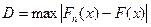 =
=0,0247 =
=0,0247
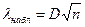 =0,247 =0,247
| 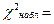 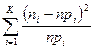 =
=6,080 =
=6,080
|
Критические значения находим в соответствующих таблицах:
 = = 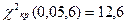 , так как , так как 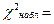 6,08< 6,08< 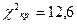 , то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично , то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично
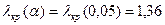 , так как , так как 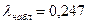 < < 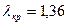 , то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова. , то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова.
Доказали, что совокупность распределена нормально, найдём оценки генеральных параметров этой совокупности.
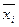 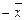
| 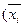 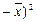 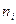
| 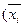 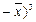 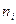
| 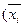 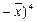 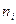
| | -6,283
| 118,428
| -744,083
| 4675,073
| | -4,712
| 155,421
| -732,344
| 3450,805
| | -3,142
| 108,59
| -341,19
| 1072,019
| | -1,571
| 39,489
| -62,037
| 97,46
| |
|
|
|
| | 1,57
| 46,833
| 73,528
| 115,439
| | 3,141
| 88,793
| 278,899
| 876,022
| | 4,172
| 222,029
| 1046,201
| 4929,699
| | 6,282
| 39,476
| 247,988
| 1557,861
| 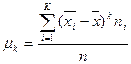
|
8,19
|
-2,33
|
167,744
|
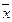
| 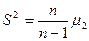
|
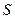
| 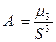
| 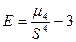
|
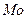
|
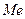
| | 11,883
| 8,274
| 2,876
| -0,0979
| -0,548
| 12,064
| 11,948
|
Найдём доверительный интервал для математического ожидания 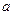 при неизвестной дисперсии при неизвестной дисперсии 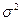 . .
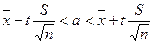 , где 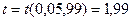 ,
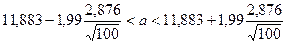 , ,
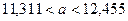
Найдём доверительный интервал для дисперсии 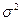 при неизвестном при неизвестном 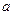 . .
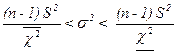 , где , где 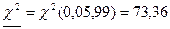 , , 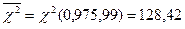 , ,
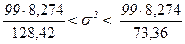 , ,
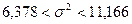 , ,
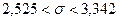 . .
Тема №4 «Корреляционно-регрессионный анализ»
Найти выборочный коэффициент корреляции и составить выборочные уравнения прямых линий регрессии 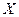 на на 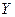 и и 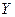 на на 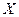 по данным корреляционной таблицы: по данным корреляционной таблицы:
Значения 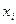 , , 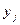 , , 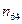 и и 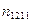 найти по формулам: найти по формулам:
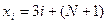 , , 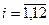 , ,
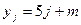 , , 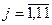 , ,
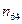 = = 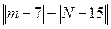 , ,
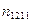 = = 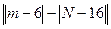 , ,
где 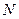 – номер студенческой группы, – номер студенческой группы, 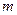 – порядковый номер фамилии студента в групповом журнале. – порядковый номер фамилии студента в групповом журнале.
Пример вычисления для студента с параметрами 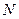 =0, =0, 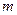 =1. =1.
По формулам вычисляем недостающие элементы.
Вычислим выборочные средние, средние квадратов, среднее произведения 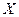 и и 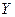 и среднеквадратические отклонения: и среднеквадратические отклонения:
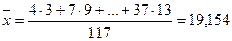 , ,
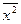 = = 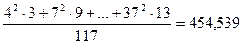 , ,
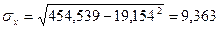 , ,
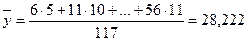 , ,
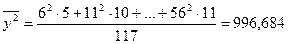 , ,
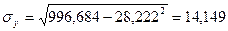 , ,
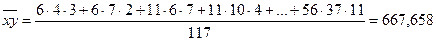 . .
Тогда 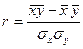 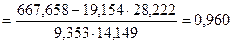 , ,
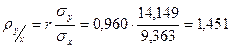 , ,
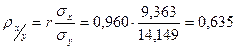 . .
Выборочное уравнение линейной регрессии 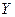 на на 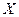 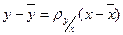 . В нашем случае . В нашем случае 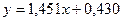 . .
Выборочное уравнение линейной регрессии 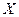 на на 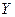 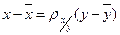 . В нашем случае . В нашем случае 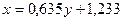 . .

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Расчет концентрации титрованных растворов с помощью поправочного коэффициента При выполнении серийных анализов ГОСТ или ведомственная инструкция обычно предусматривают применение раствора заданной концентрации или заданного титра...
Психолого-педагогическая характеристика студенческой группы
Характеристика группы составляется по 407 группе очного отделения зооинженерного факультета, бакалавриата по направлению «Биология» РГАУ-МСХА имени К...
Общая и профессиональная культура педагога: сущность, специфика, взаимосвязь Педагогическая культура- часть общечеловеческих культуры, в которой запечатлил духовные и материальные ценности образования и воспитания, осуществляя образовательно-воспитательный процесс...
|
Сущность, виды и функции маркетинга персонала Перснал-маркетинг является новым понятием. В мировой практике маркетинга и управления персоналом он выделился в отдельное направление лишь в начале 90-х гг.XX века...
Разработка товарной и ценовой стратегии фирмы на российском рынке хлебопродуктов В начале 1994 г. английская фирма МОНО совместно с бельгийской ПЮРАТОС приняла решение о начале совместного проекта на российском рынке. Эти фирмы ведут деятельность в сопредельных сферах производства хлебопродуктов.
МОНО – крупнейший в Великобритании...
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...
|
|
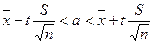 , где
, где 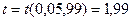 ,
,

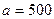 и
и  . Найти вероятность того, что объем товара в данном месяце заключен в границах от 480 до 600.
. Найти вероятность того, что объем товара в данном месяце заключен в границах от 480 до 600.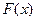 ,
, (X), если:
(X), если: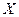 и
и 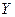 получены малые независимые выборки, объемы которых
получены малые независимые выборки, объемы которых и
и 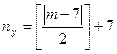 ,
,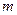 - порядковый номер фамилии студента в групповом журнале.
- порядковый номер фамилии студента в групповом журнале.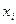 и
и 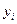 рассчитываются по формулам:
рассчитываются по формулам: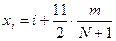 ,
, 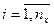 и
и 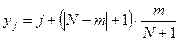 ,
, 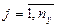 ,
, – номер студенческой группы.
– номер студенческой группы. при альтернативной гипотезе
при альтернативной гипотезе 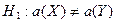 .
. =
= 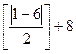 =
= 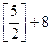 =[2,5]+8=2+8=10
=[2,5]+8=2+8=10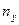 =
= 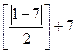 =
= 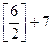 =[3]+7=3+7=10.
=[3]+7=3+7=10.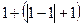 =2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11.
=2; y2=3; y3=4; y4=5; y5=6; y6=7; y7=8; y8=9; y9=10; y10=11.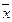 =11;
=11;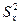 =
= 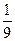 ·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)=
·(2·4,52+2·3,52+2·2,52+2·1,52+2·0,52)= 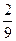 · 41,25=
· 41,25= 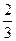 · 13,756≈9,167,
· 13,756≈9,167,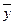 =6,5;
=6,5;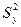 =
= 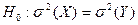 , при конкурирующей
, при конкурирующей 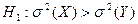 .
.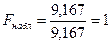 ,
, 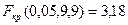 , так как
, так как 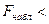
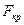 , то гипотеза о равенстве дисперсий принимается.
, то гипотеза о равенстве дисперсий принимается.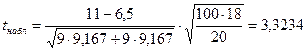 ,
, 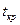 (0,05,18)=2,10, так как
(0,05,18)=2,10, так как 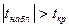 то гипотеза
то гипотеза 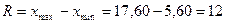 ,
,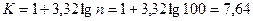 ,
,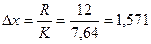 ,
,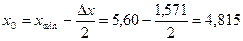 ,
,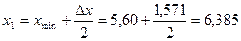 ,
,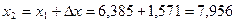 и так далее,
и так далее,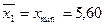 ,
,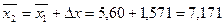 и так далее.
и так далее.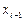
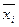
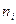
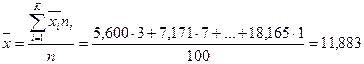 ,
, 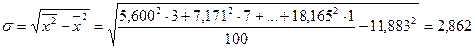 .
.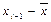
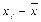
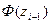
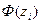
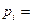
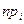
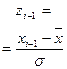
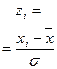
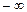
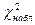 и
и 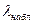 .
.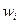
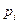
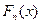
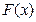
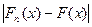
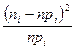
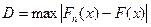 =
=0,0247
=
=0,0247
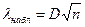 =0,247
=0,247
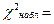
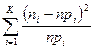 =
=6,080
=
=6,080
 =
= 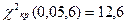 , так как
, так как 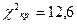 , то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично
, то принимается гипотеза о нормальном распределении генеральной совокупности, аналогично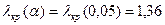 , так как
, так как 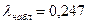 <
< 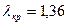 , то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова.
, то гипотеза о нормальном законе распределения подтверждается и критерием Колмогорова.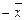
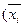
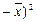
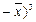
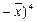
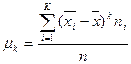
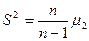
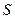
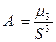
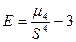
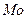
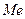
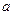 при неизвестной дисперсии
при неизвестной дисперсии 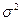 .
.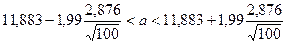 ,
,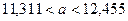
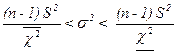 , где
, где 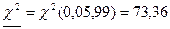 ,
, 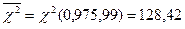 ,
,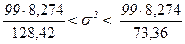 ,
,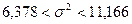 ,
,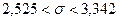 .
.
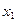
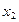
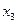
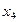
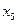
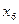

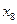
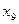
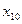
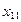
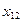
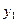

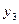
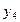
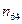
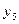
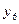
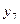
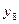
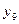
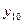
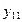
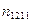
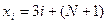 ,
, 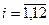 ,
,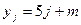 ,
, 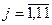 ,
,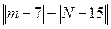 ,
,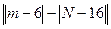 ,
,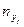
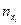
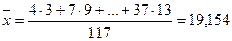 ,
,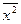 =
= 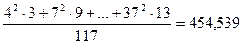 ,
,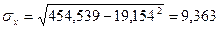 ,
,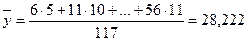 ,
,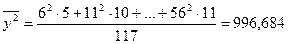 ,
,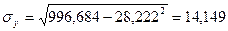 ,
,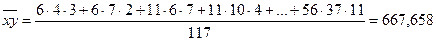 .
.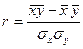
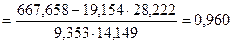 ,
,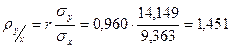 ,
,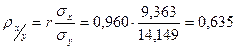 .
.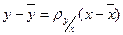 . В нашем случае
. В нашем случае 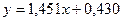 .
.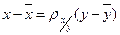 . В нашем случае
. В нашем случае 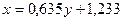 .
.


