Для студентов факультета клинической психологии
Государственное бюджетное образовательное учреждение
Курск - 2012 УДК:51(075.8) ББК:22.1я73 Т19
Рецензент: Кандидат физико–математических наук, заведующий кафедрой математического анализа и прикладной математики КГУ, Кабанко М. В.
Тарасова, С.А. Учебное пособие по математике для студентов факультета клинической психологии/ С.А. Тарасова. – Курск: ГБОУ ВПО КГМУ, 2012. – [электронное издание].
Настоящее учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования третьего поколения по специальности 030401 «Клиническая психология». В учебном пособии изложены основы теории множеств, математической логики, теории вероятностей и математической статистики применительно к психологическому профилю специализации. Для студентов психологических факультетов высших учебных заведений.
© КГМУ, 2012 Тема №1 «Элементы теории множеств» Цель: усвоить понятия множества, его элементов, конечного и бесконечного, равных множеств, научиться проводить основные операции над множествами.
Краткие теоретические сведения: Множество – одно из основных неопределяемых понятий математики. Множество – совокупность объектов, обладающих одним и тем же признаком, объекты, не входящие в эту совокупность таким признаком не обладают. Объекты множества называются его элементами. Множества обозначаются большими латинскими буквами, его элементы - маленькими. Универсальное множество Пустое множество Ø–множество, которое не содержит ни одного элемента. Способы задания множеств: 1) перечислением элементов – 2) указанием характеристического свойства – Если множество содержит конечное число элементов, то оно называется конечным, иначе множество называется бесконечным. Если каждый элемент множества Свойства подмножеств: 1) 2) Ø Множества Всякое подмножество Объединением множеств Пересечением множеств Разностью множеств Геометрически операции над множествами изображаются с помощью диаграмм Эйлера – Венна:
Свойства операций над множествами: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) Пример. Доказать свойство Решение. Пусть Пусть Так как Множество, рассматриваемое вместе с каким-нибудь установленным в нём порядком следования элементов, называется упорядоченным множеством. Основные числовые множества: 1) 2) 3) 4) 5) 6) Между множествами Если множества эквивалентны, то они имеют одинаковую мощность или кардинальное число Мощность конечного множества равна числу элементов этого множества. Мощность пустого множества равна нулю. Бесконечное множество называется счётным, если оно эквивалентно множеству натуральных чисел. Бесконечное множество, мощность которого превышает мощность счётного множества, называется несчётным. Множество действительных чисел несчётно и его мощность называется мощностью континуума. Пусть имеются два множества Пример. Пусть
Нечётким множеством Пример. Математико-психологический портрет группы студентов 1-го курса факультета клинической психологии по степени принадлежности каждого из них к множеству трудолюбивых людей.
Объединением нечётких множеств Пересечением нечётких множеств Лингвистическая переменная – переменная, значениями которой являются слова или предложения естественного или искусственного языков. Контрольные вопросы: 1. Понятие множества и его элементов. Способы задания множеств. 2. Конечное и бесконечное множества. 3. Подмножество. Свойства подмножеств. 4. Операции над множествами. 5. Основные числовые множества. 6. Мощность множества. Счётное и несчётное множества. 7. Декартово произведение множеств. 8. Нечёткие множества. Пример. 9. Операции над нечёткими множествами. 10. Понятие лингвистической переменной. Контрольные задания: 1. Определить является ли одно из множеств а) б) 2. Какие из элементов множества 3. Для двухэлементного множества 4. Найти объединение, пересечение, разность и декартово произведение множеств а) б) 5. Найти объединение, пересечение и разность следующих промежутков: а) [3;7), (4;9], б) (- в) [1;10], (-7;4]. 6. Доказать и с помощью диаграмм Эйлера-Венна проверить: а) б) в) ( г) ( 7. Решить задачу: Из 32 учеников класса 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 – и в той, и в другой. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секциях. Задания для домашней работы: 1. Найти объединение, пересечение, разность и декартово произведение множеств а) б) 2. Доказать и с помощью диаграмм Эйлера-Венна проверить: а) ( б) в) ( 3. Найти объединение, пересечение и разность следующих промежутков: а) (-1;3), [2;+ б) [1;4), [2;3], в) [1;3), [5; +
Тема №2 «Элементы математической логики» Цель: научиться приводить дизъюнктивные и конъюнктивные нормальные формы к совершенным дизъюнктивным и конъюнктивным нормальным формам, используя логические равносильности; применять законы математической логики для решения логических задач; применять язык логики предикатов для записи математических предложений, определений, построения противоположных утверждений. Краткие теоретические сведения: Высказывание – любое повествовательное предложение, которому можно приписать истинностное значение. Предложение, которое содержит хотя бы одну переменную и становится высказыванием при подстановке вместо всех переменных их значений, называется высказывательной формой. Высказывание, представляющее собой одно утверждение, называется элементарным. Высказывание, образованное из элементарных с помощью логических связок «и», «или», «если, то», «не», называется составным (сложным). Образование составного высказывания из элементарных называется логической операцией. Логическая операция, соответствующая логической связке «не» («неверно, что») называется отрицанием:
Логическая операция, соответствующая логической связке «и», называется конъюнкцией:
Логическая операция, соответствующая логической связке «или», называется дизъюнкцией:
Логическая операция, имеющая вид «если
Логическая операция, соответствующая сложному союзу «тогда и только тогда, когда», называется эквиваленцией:
Приоритет логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Под формулой 1) всякое элементарное высказывание есть формула, 2) если 3) других формул, кроме перечисленных в 1) и 2), нет. Две формулы называются равносильными, если их таблицы истинности совпадают: Основные формулы математической логики: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) Примеры. 1) Доказать формулу Решение.
Видим, что средний столбик состоит из одних единиц, равносильность доказана. 2) Упростить формулу Решение.
Формула называется тождественно – истинной (тавтологией) (тождественно – ложной (противоречием)), если её истинностное значение «истина» («ложь») при любых возможных значениях переменных. Предложение Если предложение Если Дизъюнктивная нормальная форма (ДНФ) представляет собой дизъюнкцию конъюнкций переменных и их отрицаний, либо конъюнкцию самих переменных. Конъюнктивная нормальная форма (КНФ) представляет собой конъюнкцию дизъюнкций переменных и их отрицаний, либо дизъюнкцию самих переменных. Любую формулу можно привести к ДНФ или к КНФ. Совершенная дизъюнктивная нормальная форма (СДНФ) – дизъюнкция конъюнкций, содержащих все исходные переменные (с отрицанием или без). Совершенная конъюнктивная нормальная форма (СКНФ) – конъюнкция дизъюнкций, содержащих все исходные переменные (с отрицанием или без). Пример. Привести к ДНФ формулу Решение.
Функция, все значения которой принадлежат множеству {0; 1} называется предикатом: Предикат с Подмножество области определения предиката, состоящее из тех и только тех элементов, которым соответствует истинное значение предиката, называется областью истинности предиката. Если область истинности предиката совпадает со всей областью определения, то предикат называется тождественно – истинным. Если же область истинности представляет собой пустое множество, то предикат называется тождественно – ложным. Всякий одноместный предикат Кванторы: 1) 2) 3) Контрольные вопросы: 1. Высказывание. Простые и составные высказывания. Высказывательная форма. 2. Операции алгебры логики: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция и их свойства. 3. Формула алгебры логики. Равносильные формулы алгебры логики. Тавтология. Противоречие. 4. Основные равносильности. 5. Виды теорем. Необходимое и достаточное условия. 6. Элементарная конъюнкция. Дизъюнктивная нормальная форма (ДНФ). Совершенная дизъюнктивная нормальная форма (СДНФ). 7. Элементарная дизъюнкция. Конъюнктивная нормальная форма (КНФ). Совершенная конъюнктивная нормальная форма (СКНФ). 8. Предикат. Область истинности предиката. Контрольные задания: 1. Доказать тождественную истинность основных формул математической логики. 2. Упростить: а) б) в) (( г) ( 3. Привести формулу 4. Решить задачу: По подозрению в совершённом преступлении задержали Брауна, Джона и Смита. Один из них был уважаемым в городе стариком, другой был малоизвестным чиновником, третий – известным мошенником. В процессе следствия старик говорил правду, мошенник лгал, а третий задержанный в одном случае говорил правду, а в другом – ложь. Вот что они утверждали: Браун: «Я совершил это. Джон не виноват», Джон: «Браун не виноват. Преступление совершил Смит», Смит: «Я не виноват, виноват Браун». Определить имя старика, мошенника и чиновника и кто из них виноват, если известно, что преступник один. 5. Найти область истинности предиката а) область определения б) в) 6. Записать на языке логики предикатов определения: а) периодической функции, б) чётной функции, в) построить отрицания определений в примерах а) и б). Задания для домашней работы: 1. Доказать равносильность следующих формул: 2. Решить задачу: Известно, что если Джонс не встречал ночью Смита, то Смит – убийца. Джонс говорит неправду или Смит не убийца. Джонс говорит правду. Верно ли, что Джонс встретил ночью Смита. 3. Найти область истинности предиката
Тема №4 «Вычисление вероятностей случайных событий» Цель: усвоить основные понятия теории вероятностей – достоверные, невозможные, случайные события; совместные и несовместные события; научиться использовать классическое, статистическое и геометрическое определения вероятности. Краткие теоретические сведения: Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях. Опытом (испытанием) называется всякое осуществление определённого комплекса условий или действий, при которых наблюдается соответствующее явление. Событием называется всякий возможный факт, который в результате опыта может произойти или не произойти. Обозначаются большими латинскими буквами. Достоверным Невозможным Ø называют событие, которое в данном опыте не может произойти. Случайным называют событие, которое в данном опыте может произойти, но может и не произойти. Два события A и B называются несовместными, если в данном испытании они не могут произойти вместе. Два события A и B называются совместными в данном испытании, если появление одного из них не исключает возможность появления другого события в этом же испытании. Несколько событий образуют полную группу, если они несовместны и единственно возможные исходы испытания. Если в полной группе только два события, то они называются противоположными. Исход опыта называется благоприятствующим некоторому событию, если его появление влечет за соб
|


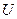 (универсум) – множество, которому принадлежат все те элементы, которые допустимо рассматривать при решении данной задачи.
(универсум) – множество, которому принадлежат все те элементы, которые допустимо рассматривать при решении данной задачи.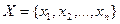 ,
,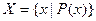 .
.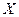 является элементом множества
является элементом множества 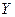 , то множество
, то множество 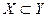 .
.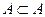 ,
,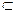
 .
.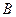 называются равными, если они состоят из одних и тех же элементов:
называются равными, если они состоят из одних и тех же элементов: 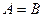 .
.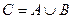 , состоящее из элементов множеств
, состоящее из элементов множеств 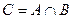 , состоящее из элементов, одновременно принадлежащих множеству
, состоящее из элементов, одновременно принадлежащих множеству 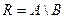 , состоящее из элементов
, состоящее из элементов 
 ,
,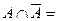 Ø,
Ø,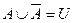 ,
,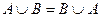 ,
,  - коммутативность,
- коммутативность,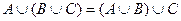 ,
, 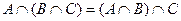 - ассоциативность,
- ассоциативность,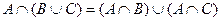 ,
, 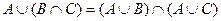 - дистрибутивность,
- дистрибутивность,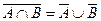 ,
, 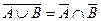 - законы де Моргана,
- законы де Моргана,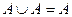 ,
, 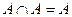 ,
,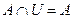 ,
, 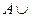 Ø
Ø 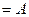 ,
,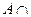 Ø = Ø,
Ø = Ø, 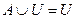 ,
,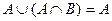 ,
, 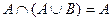 - законы поглощения.
- законы поглощения.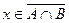 , тогда
, тогда 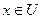 и
и 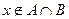 , то есть либо
, то есть либо 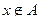 , либо
, либо 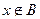 . В первом случае
. В первом случае 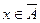 , но тогда
, но тогда 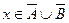 ; во втором случае
; во втором случае 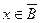 , но тогда
, но тогда 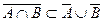 .
.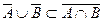 .
.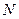 – натуральные,
– натуральные,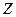 – целые,
– целые,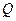 - рациональные,
- рациональные,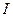 – иррациональные,
– иррациональные,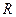 – действительные,
– действительные,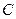 – комплексные числа.
– комплексные числа.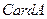 .
.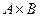 есть множество всех упорядоченных пар
есть множество всех упорядоченных пар 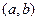 , в которых первый элемент принадлежит множеству
, в которых первый элемент принадлежит множеству 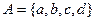 ,
, 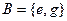 . Тогда
. Тогда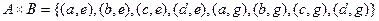 .
.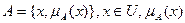 – степень принадлежности
– степень принадлежности 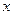 множеству
множеству 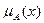
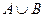 с функцией принадлежности
с функцией принадлежности 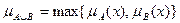 .
.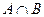 с функцией принадлежности
с функцией принадлежности 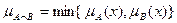 .
.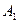 и
и 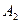 собственным подмножеством другого:
собственным подмножеством другого: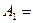 {1,{1,2}},
{1,{1,2}}, 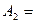 {{1,2},2},
{{1,2},2},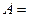 {Ø,{Ø},{1}}?
{Ø,{Ø},{1}}?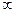 ;5], (0;+
;5], (0;+ 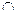
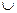
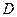 ) = (
) = (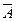 . Отрицание истинно, когда основное высказывание ложно.
. Отрицание истинно, когда основное высказывание ложно.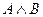 . Конъюнкция истинна, когда истинны оба высказывания.
. Конъюнкция истинна, когда истинны оба высказывания.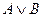 . Дизъюнкция ложна, когда ложны оба высказывания.
. Дизъюнкция ложна, когда ложны оба высказывания.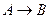 . Высказывание
. Высказывание 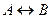 . Эквиваленция истинна, когда оба высказывания одновременно истинны или одновременно ложны.
. Эквиваленция истинна, когда оба высказывания одновременно истинны или одновременно ложны.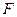 логики высказываний понимается следующее:
логики высказываний понимается следующее: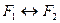 .
.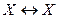 - закон тождества,
- закон тождества,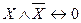 - закон противоречия,
- закон противоречия,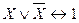 - закон исключённого третьего,
- закон исключённого третьего,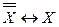 - снятие двойного отрицания,
- снятие двойного отрицания,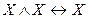 ,
, 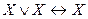 - идемпотентность,
- идемпотентность,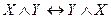 ,
, 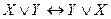 - коммутативность,
- коммутативность,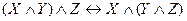 ,
, 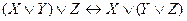 - ассоциативность,
- ассоциативность,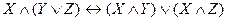 ,
, 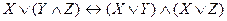 - дистрибутивность,
- дистрибутивность,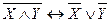 ,
, 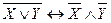 - законы Де Моргана,
- законы Де Моргана,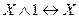 ,
, 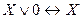 ,
, 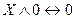 ,
, 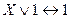 - сочленение переменной с константой,
- сочленение переменной с константой,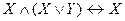 ,
, 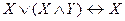 - законы поглощения,
- законы поглощения,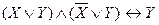 ,
,  - законы склеивания,
- законы склеивания,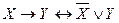 ,
, 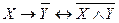 - замена импликации,
- замена импликации,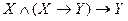 - правило modus ponens,
- правило modus ponens,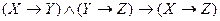 - правило силлогизма,
- правило силлогизма,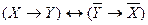 - закон контрапозиции,
- закон контрапозиции,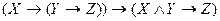 - соединение посылок,
- соединение посылок,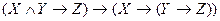 - разъединение посылок.
- разъединение посылок.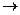
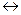
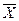
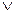
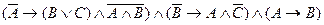 .
.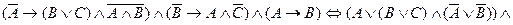
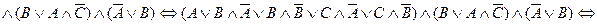
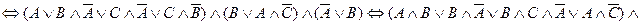
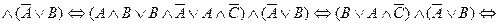
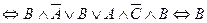 .
.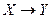 называется прямым утверждением,
называется прямым утверждением, 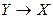 - обратным,
- обратным, 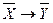 - противоположным,
- противоположным, 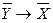 - обратнопротивоположным.
- обратнопротивоположным.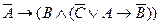 .
.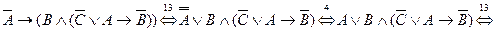
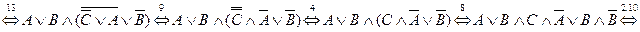
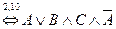 .
.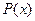 ,
, 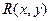 .
.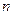 различными переменными называется
различными переменными называется 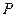 , называется объёмом данного свойства. Многоместные предикаты выражают отношения.
, называется объёмом данного свойства. Многоместные предикаты выражают отношения.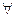 - квантор всеобщности,
- квантор всеобщности,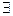 - квантор существования,
- квантор существования,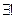 - квантор существования единственности.
- квантор существования единственности.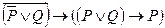 ,
,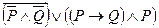 ,
,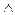 (
(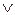
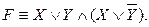
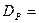 {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},
{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},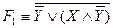 и
и 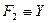 .
.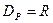 .
.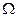 называют событие, которое обязательно произойдет в данном опыте.
называют событие, которое обязательно произойдет в данном опыте.


