Теорема умножения вероятностей
Вероятность совместного наступления двух независимых событий A и B равна произведению вероятностей этих событий P(AB)=P(A)·P(B). Вероятность совместного наступления двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло Пример. Два стрелка делают одновременно по одному выстрелу в одну цель. Какова вероятность того, что оба попадут, если известно, что первый стрелок в среднем дает 7 попаданий, а второй 8 попаданий на каждые 10 выстрелов? Какова вероятность поражения мишени? Решение. Вероятность попадания первого стрелка (событие A) равна P(A) =0,8, вероятность попадания второго стрелка (событие B) равна P(B) =0,7. События A и B независимы друг от друга, поэтому вероятность совместного наступления этих событий (совместное попадание в цель) найдем по теореме умножения для независимых событий: P(AB)=P(A)P(B) =0,8·0,7=0,56. Вероятность поражения мишени означает попадание в мишень хотя бы одного стрелка. Так как попадание в мишень первого и второго стрелков являются событиями совместными, то применение теоремы сложения вероятностей для совместных событий дает следующий результат: P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)·P(B) =0,8+0,7- 0,8·0,7=0,94. Формула полной вероятности: Если случайные события Н1,Н2,...,Нn образуют полную группу, и если событие А может осуществляться только совместно с каким-нибудь одним из этих событий, то вероятность наступления события А можно определить по формуле:
Пример. В деканат поступили результаты тестирования по трём предметам в соотношении 2:3:5. При этом вероятности неудовлетворительной оценки по каждому из этих предметов соответственно равны 0,05, 0,02 и 0,08. Определить вероятность того, что взятая наугад работа окажется неудовлетворительной. Решение. Пусть Тогда Формулы Байеса: Пример. Используя данные предыдущей задачи, определить вероятность того, что оказавшаяся неудовлетворительной работа – это работа по второму тесту. Решение. Контрольные вопросы: 1. Сумма и произведение событий. 2. Свойства операций над событиями. 3. Теорема сложения вероятностей для несовместных событий и следствия из нее. 4. Теорема сложения вероятностей для совместных событий. 5. Условная вероятность. Зависимые и независимые события. 6. Теорема о вероятности произведения двух независимых событий. 7. Теорема умножения вероятностей для зависимых событий. 8. Формула полной вероятности (формула гипотез). 9. Формулы Байеса. Контрольные задания: 1. На семи карточках написаны буквы А, А, А, Б, Б, Н, Р. Карточки перемешиваются и раскладываются случайным образом. Какова вероятность того, что получится слово БАРАБАН? 2. Два стрелка независимо друг от друга производят по одному выстрелу по мишени. Известно, что вероятность попадания первого – 0,9, второго – 0,8. Найти вероятность того, что а) оба стрелка попадут в мишень, б) хотя бы один стрелок попадёт в мишень. 3. Зашедший в магазин мужчина что-нибудь покупает с вероятностью 0,1, а женщина – с вероятностью 0,6. У прилавка один мужчина и две женщины. Какова вероятность того что, по крайней мере, одно лицо что-нибудь купит? 4. В семье трое детей. Считая рождение мальчика и девочки равновероятными, найти вероятность того, что в семье все мальчики. 5. Студент выучил лишь один билет из 30 экзаменационных. Определить, зависит или нет вероятность извлечения «счастливого билета» от того, первым, вторым или третьим выбирает студент свой билет. 6. В двух группах занимаются соответственно 20 и 30 студентов, причем в первой группе 5 юношей, а во второй – 3. Какова вероятность того, что выбранный наугад студент – юноша? 7. Для примера 6 определить вероятность того, что выбранный студент учится в первой или во второй группе, если известно, что он – юноша? 8. Охотник сделал три выстрела по кабану. Вероятность попадания первым выстрелом равна 0,4, вторым – 0,5, третьим – 0,7. Одним попаданием кабана можно убить с вероятностью 0,2, двумя – 0,6, тремя – 1. Найти вероятность того, что кабан будет убит. Задания для домашней работы: 1. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность разрушения моста, если на него сбросить 4 бомбы, вероятности попадания которых соответственно равны: 0,3, 0,4, 0,6 и 0,7. 2. Из трех орудий произведен залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8, для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность того, что: а) только один снаряд попадет в цель, б) только два снаряда попадут в цель, в) все три снаряда попадут в цель, г) хотя бы один снаряд попадет в цель. 3. В первой урне 1 белый и 9 черных шаров, во второй – 1 черный и 5 белых. Из каждой урны выбираем наугад по одному шару, а оставшиеся ссыпаем в третью урну, из которой наугад вынули 1 шар. Найти вероятность того, что: а) шар, вынутый из третьей урны, будет белым, б) из обеих урн вынули белые шары, если шар, вынутый из третьей урны, оказался белым. 4. В швейной мастерской работают 3 мастера, производительности труда которых относятся как 5:6:7. Для первого мастера вероятность изготовления изделия отличного качества равна 0,95, для второго и третьего мастеров эти вероятности соответственно равны 0,8 и 0,9. Изготовленное изделие оказалось отличного качества. Найти вероятность того, что его изготовил третий мастер.
|

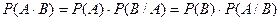 .
.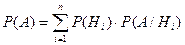 ,
, 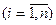
 - событие, состоящее в том, что взятая наугад работа по i-му предмету. Тогда по условию
- событие, состоящее в том, что взятая наугад работа по i-му предмету. Тогда по условию  . Событие А состоит в том, что взятая наудачу работа – неудовлетворительная. По условию
. Событие А состоит в том, что взятая наудачу работа – неудовлетворительная. По условию 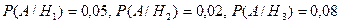 .
.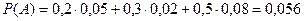 .
.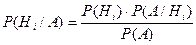 ,
, 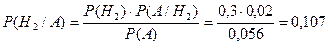 .
.


