Найти производную второго порядка
3. Найти значение у ”(x) в точке х0
, x0 =
4.Вычислить полный дифференциал первого порядка
5. Для функции:
Вычислить: а)
6. Материальная точка движется по закону s(t)= (м). Найти скорость и ускорение точки в момент времени t= с.
7. Найти момент времени, в который скорость точки будет равна м/с.
8. Составить уравнение касательной и нормали к графику функции у= в точке х0 =. Выполнить чертёж.
3.2. Допуск к работе
3.2.1. В чём заключается механический смысл производной? ____________________________________________________________________________________________________________________________________________________________
3.2.2. Как вывести на экран панель математических инструментов (Math Palette)? ____________________________________________________________________________________________________________________________________________________________
3.2.3. Как можно вычислить производную функции, используя математическую панель в MathCAD? ____________________________________________________________________________________________________________________________________________________________
3.2.4. Как можно вычислить производную функции, используя горизонтальное меню? ____________________________________________________________________________________________________________________________________________________________
3.2.5. Что нужно сделать для вычисления производной функции в заданной точке? ____________________________________________________________________________________________________________________________________________________________
3.2.6. Как находятся производные высших порядков для заданной функции? ____________________________________________________________________________________________________________________________________________________________
3.2.7. Что необходимо сделать, чтобы решить уравнение с помощью пакета MathCAD? ____________________________________________________________________________________________________________________________________________________________
3.2.8. Как вычислить смешанную частную производную с помощью пакета MathCAD? __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3.2.9. Каким образом строится график с помощью пакета MathCAD? ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3.2.10 Как построить два графика в одной системе координат с помощью пакета MathCAD? ____________________________________________________________________________________________________________________________________________________________
К работе допускается ______________
4. Результаты работы
4.1.
4.2
4.3
4.4
4.5
А)
Б)
В)
4.6
v = _____________________ a = _______________________
4.5 t = ________________________
4.6
f(x0) =
f ‘ (x) =
f ‘ (x0) =
Уравнение касательной y = f(x0) + f ‘ (x0) (x - x0)
_________________________________________________________________
_________________________________________________________________
5. Вывод
В ходе выполнения данной работы ________________________________________________________________________________________________________________________________________________________________________________________________________________________
ПРАКТИЧЕСКАЯ РАБОТА 11
Нахождение неопределённых, определённых и несобственных интегралов.
1. Цель работы
1. 1 Научиться вычислять определённые и неопределённые интегралы методом подстановки
2. Ход работы
2.1. Вариант
Найти неопределённые интегралы:
Найти определённые интегралы:
Найти несобственные интегралы:
2.2.1 Заполните таблицу интегралов
1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
2.2.2. Заполните таблицу:
2.2.3. Выпишите формулу Ньютона - Лейбница ___________________________________________________________________________________________________________________________________________________________________________________________________________________________ 2.2.4 Заполните таблицу:
2.2.5 По какой формуле вычисляется интеграл ________________________________________________________________________________________________________________________________________________
2.2.6 По какой формуле вычисляется интеграл ________________________________________________________________________________________________________________________________________________
2.2.7 По какой формуле вычисляется интеграл ________________________________________________________________________________________________________________________________________________
2.2.8 По какой формуле вычисляется интеграл ________________________________________________________________________________________________________________________________________________
К работе допускается ______________
3. Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 12
Решение прикладных задач с помощью определённого интеграла в Mathcad
1. Цель работы
1.1. Научиться применять определённый интеграл для решения геометрических задач. 1.2. Научиться применять определённый интеграл для решения физических задач.
2. Оборудование
Пакет программ MathCAD.
3. Ход работы
3.1 Вариант
3.1.1. Скорость движения тела задаётся формулой
3.1.2. Вычислить силу давления на прямоугольную пластину с основанием см и высотой см, погружённую вертикально в жидкость плотностью
3.1.3. Силой
3.1.4. Найти объём тела, полученного при вращении кривой вокруг оси Ох, если
3.1.5. Найти площадь поверхности, полученной при вращении кривой вокруг оси Ох, если
3.1.6. Найти длину кривой между точками
3.1.7. Пластина в виде треугольника с основанием см и высотой см погружена в жидкость, плотности
3.1.8. Найти площадь фигуры, ограниченной линиями: , если
3.2 Допуск к работе
3.2.1. В чём заключается геометрический смысл определённого интеграла? _______________________________________________________________________________________________________________________________________________
3.2.2. Как вычислить площадь плоской фигуры, ограниченной графиками двух функций? _______________________________________________________________________
3.2.3. Как вычислить длину дуги плоской кривой? _______________________________________________________________________
3.2.4. Какую поверхность называют поверхностью вращения? _______________________________________________________________________________________________________________________________________________
3.2.5. _______________________________________________________________________
3.2.6. Как находится площадь поверхности фигуры, полученной при вращении вокруг оси _______________________________________________________________________
3.2.7 В чём заключается физический смысл определённого интеграла? _______________________________________________________________________________________________________________________________________________
3.2.8 Как вычислить путь, пройденный телом при равномерном движении? _______________________________________________________________________________________________________________________________________________
3.2.9 Как вычислить путь, пройденный телом при неравномерном движении? ________________________________________________________________________________________________________________________________________________
3.2.10 Как вычислить работу переменной силы? ________________________________________________________________________________________________________________________________________________
3.2.11 Как вычислить силу давления жидкости на вертикально расположенную пластину? ________________________________________________________________________________________________________________________________________________ 3.2.12 Как строится в MathCAD график функции? ________________________________________________________________________________________________________________________________________________________________________________________________________________________
3.2.13 Как форматируется в MathCAD график функции? ________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________
3.2.15 Как в MathCAD вычисляются определённые интегралы? ________________________________________________________________________________________________________________________________________________________________________________________________________________________
К работе допускается ______________
4. Результаты работы
4.1.
4.2.
Р=
4.3. Cилой F= Н пружина растягивается на ∆x см = м Коэффициент жёсткости пружины Пружина растягивается на b = см = м
k: = k =
A=
4.4 – 4.5
4.6
L =
4.8
S=
5. Вывод
В ходе выполнения данной работы ________________________________________________________________________________________________________________________________________________________________________________________________________________________
Вычисление двойных интегралов
1. Цель работы
Научиться вычислять двойные интегралы по прямоугольной и по произвольной области.
2. Ход работы
2.1 Вариант Вычислить интегралы:
1)
Д: ≤ х ≤, ≤ у ≤. 2) 3)
4)
Д:
5)
Д:
6) Изменить порядок интегрирования:
2.2 Допуск к работе
|

 ; б)
; б)  ; в)
; в) 

 Уравнение нормали y = f(x0) -
Уравнение нормали y = f(x0) -  (x - x0)
(x - x0)
 2.2. Допуск к работе
2.2. Допуск к работе










 x+8
x+8

 x - 5
x - 5
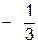 x + 7
x + 7





 ?
? ?
? , если
, если  - особая точка?
- особая точка? - особая точка?
- особая точка? . Найти путь пройденный телом за сек.
. Найти путь пройденный телом за сек.
 так, что верхнее основание находиться на см ниже поверхности жидкости.
так, что верхнее основание находиться на см ниже поверхности жидкости. Н пружина растягивается на см. Первоначальная длина пружины равна см. Какую работу надо совершить, чтобы растянуть пружину до см?
Н пружина растягивается на см. Первоначальная длина пружины равна см. Какую работу надо совершить, чтобы растянуть пружину до см? кривой
кривой  ?
?














 V=
V=

 S=
S=


 Основание AC = см = м
Высота BD = см = м
Основание AC = см = м
Высота BD = см = м


 Р=
Р= 



 ПРАКТИЧЕСКАЯ РАБОТА 13
ПРАКТИЧЕСКАЯ РАБОТА 13 , если
, если





