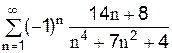Алгоритм решения дифференциального уравнения с разделяющимися переменными
1) Выразить производную функции через дифференциалы 2) Члены с одинаковыми дифференциалами перенести в одну сторону равенства и вынести дифференциал за скобку. () d __ = () d ___ 3) Разделить переменные. (f(____)) d __ = (f(____)) d ___ 4) Проинтегрировать обе части равенства и найти общее решение. 5) Если заданы начальные условия, то найти частное решение.
2.3.4 Выберите дифференциальное уравнение, полученное в результате разделения переменных А) Ответ: __________
2.3.5 Дано дифференциальное уравнение: А) Ответ: __________
2.3.6 А) В) Ответ: __________
2.3.7 Дифференциальное уравнение первого порядка вида:
___________________________ называется однородным, если 2.3.8 Однородное дифференциальное уравнение приводится к дифференциальному уравнению с разделяющимися переменными
подстановкой ___ y = _______________________
тогда ___ y ‘ = _________________________, _____
2.3.9 Дифференциальное уравнение первого порядка вида: _________________________________, где
2.3.10 Заполните пропуски Алгоритм решения линейного дифференциального уравнения первого порядка 1 Привести уравнение к виду 2 Используя подстановку 3 Сгру 4 Найти функцию 5 Подставить найденную функцию в оставшееся выражение и найти вторую функцию. 6 Записать общее решение, подставив выражения для найденных функций 7 Если требуется найти частное решение, то определить С из начальных условий и подставить в общее решение.
К работе допускается ______________
3. Результаты работы
Решение дифференциальных уравнений второго порядка
4. Цель работы
1.1 Научиться решать дифференциальные уравнения второго порядка, допускающие понижение порядка. 1.2 Научиться решать линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 1.3 Научиться применять дифференциальные уравнения к решению физических задач
5. Ход работы
2.1 Вариант
Найдите общее решение дифференциального уравнения:
1) _____________________________________________
2) ______________________________________________
Найдите частное решение дифференциального уравнения:
3) ______________________________________________
______________________________________________
4) _______________________________________________________________________________
Найдите закон движения точки:
5) _______________________________________________________________________________
6)________________________________________________________________________________
2.2 Допуск к работе 2.2.1 Решите уравнение
2.2.2 Вычислите
2.2.3 Продолжите равенства: a) ln 5 + ln 4 = ln 5∙4 = ln _____ б) ln(x+3) + lnC = _____________________ в) ln 12 = b ↔ 12 = e b г) ln z = 5x + 8 ↔ z = д) е) 2.2.4 Заполните таблицу:
К работе допускается ______________
6. Результаты работы
Применение дифференциальных уравнений для решения прикладных задач
1. Цель работы
1.1 Научиться применять дифференциальные уравнения для решения прикладных задач
2. Ход работы
2.1 Вариант 1) Для некоторой компьютерной фирмы функция маржинальной выручки от продажи своей продукции имеет вид MR =. Здесь MR – маржинальная выручка фирмы, а q – объем продукции. Маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж. Найти функцию общей выручки. Используя полученную функцию определить: а) общую выручку, если объём продукции q = штук. б) объём продукции, который принесёт выручку тысяч рублей.
2) Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости. Начальная стоимость равна тыс.руб, стоимость его через год составила тыс. руб. Запишите формулу для вычисления стоимости оборудования. Используя полученную формулу определить: а) какова будет стоимость оборудования через года; б) через сколько лет стоимость оборудования составит тыс. рублей.
3) Сумма тыс. руб. положена в сберегательную кассу на % в год. Найти закон изменения суммы при условии, что приращение начисляется непрерывно и скорость приращения вклада прямо пропорциональна первоначальной величине вклада. Используя полученный закон определить: а) величину вклада через года; б) через сколько лет величина вклада составит тыс. рублей.
4) Цена на планшеты некоторой фирмы составляет 13 тыс. рублей. Спрос s и предложение q определены соотношениями: q = p’ + p +, s = 2p’+ p +, где p’ – тенденция формирования цены (производная цены по времени). Определите формулу, по которой должна изменятся цена, чтобы спрос соответствовал предложению. Используя полученную формулу определить: а) цену планшета через месяца; б) через сколько месяцев цена планшета будет тыс. рублей.
5) В магазине компьютерной техники начали продажу новой модели смартфона, ежедневно продавали по смартфона. Анализ рынка показал, что можно продавать по смартфонов в день. Через 1 месяц после начала рекламной компании стали продавать по смартфонов в день. Считая скорость роста продажи смартфонов пропорциональной разности между предельным значением объёма продаж (насыщенным спросом) и её текущим значением, записать закон изменения количества ежедневно продаваемых смартфонов от времени, прошедшего с начала рекламной компании. Используя полученный закон определить: а) объём продаж через месяца после начала рекламной компании б) через сколько месяцев после начала рекламной компании объём продаж составит смартфонов. 2.2
2.2.1 Известно, что S = C∙e kt и при t = 0 S = 14. Найдите С
__________________________________________________________________________________
2.2.2 Известно, что S = 14∙e kt и при t = 1 S = 28. Найдите e k
__________________________________________________________________________________
2.2.3 Известно, что сумма в 300 тыс. рублей положена под 7% годовых. Найдите сумму вклада через год __________________________________________________________________________________
2.2.4 Известно, что -ln(6-p) = t + C выразите р
__________________________________________________________________________________
__________________________________________________________________________________
2.2.5 Известно, что Р = 7 + 14∙e kt и при t = 1 Р = 49. Найдите e k
__________________________________________________________________________________
2.2.6 Известно, что р = 40 - C∙e -kt и при t = 0 р = 50. Найдите С
__________________________________________________________________________________
2.2.7 Известно, что р = 40 - 3∙e -kt и при t = 1 р = 70. Найдите e k
__________________________________________________________________________________
2.2.8 Из условия: «Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости.», получим:
__________S’ = S _______________________________
2.2.9 Из условия: «Скорость приращения вклада прямо пропорциональна первоначальной величине вклада», получим:
__________ ’ = k _________________________
2.2.10 Из условия: «Считая скорость роста продажи смартфонов пропорциональной разности между предельным значением объёма продаж (насыщенным спросом равным 200) и её текущим значением», получим __________ p’ = (-p) ∙ k ________________
К работе допускается ______________
3. Результаты работы ПРАКТИЧЕСКАЯ РАБОТА 17
Решение дифференциальных уравнений в Mathcad
1. Цель работы
2. Оборудование
Пакет программ MathCAD.
3. Ход работы
3.1 Вариант
найти закон изменения скорости и закон движения тела, если
при t = 0, S = _________, v = ______________
на отрезке [; ], разбив его на ______ частей, если у() =
на отрезке [; ], разбив его на ______ частей, если у() =
на отрезке [; ], разбив его на ______ частей, если у() =
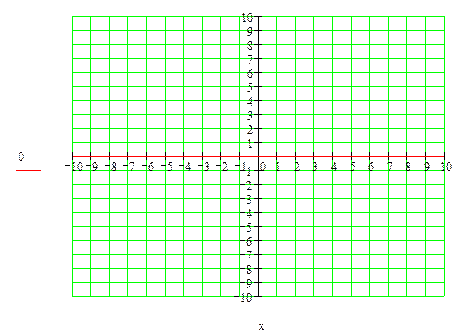
Постройте в одной системе координат график приближённого и точного аналитического решения у =
3.2. Допуск к работе
4.2.1. Разделите переменные ____________________________________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________________________________
4.2.2. Комбинацией каких клавиш вызывается в документе MathCAD команда символьных операций (→)? ____________________________________________________________________________________________________________________________________________________________
4.2.3. Пусть y’ = z, тогда y ” =?
4.2.4. Известно, что S(t) = 15t2 + 4t + C и при t = 2, S = 10. Найти С ____________________________________________________________________________________________________________________________________________________________
4.2.5. Продолжите равенства a(t) = v ‘ (t) = v (t) = S ‘ (t) = 4.2.6. Известно, что отрезок [2;3] разбили на 10 частей продолжите ряд
2; _______________________________________________________________
4.2.7. Известно, что отрезок [4;7] разбили на 6 частей продолжите ряд
2; _______________________________________________________________
4.2.8. Комбинацией каких клавиш MathCAD вызывается знак «жирного» равенства? ____________________________________________________________________________________________________________________________________________________________
4.2.9. Как на панели матриц выглядит клавиша для вывода на экран двоеточия в MathCAD (2.. 3)? ____________________________________________________________________________________________________________________________________________________________
4.2.10 С помощью какой закладки мастера форматирования графиков можно изменить внешний вид линии графика (например сделать его точечным)? ____________________________________________________________________________________________________________________________________________________________
К работе допускается ______________
4. Результаты работы
2.
dy(x,C1) =
y(x,C1,C2) =
3. Характеристическое уравнение:
Корни характеристического уравнения: k1 = k2 =
Общее решение уравнения:
Поверка правильности решения: (запись с экрана)
4.
v(t,C1) =
C1 =
S(t,C1,C2) =
C2 =
S(t,C1,C2) =
given
___________________ = ________________ y() = ____
y:= odesolve (x,___, _____)
x:= ____, ______.. ____
x = y(x)=
6. y:=
F(x,y):=
y1:=rkfixced(y,___, ____, ____, F y1= 7. given
___________________ = ________________ y() = ____
y:= odesolve (x,___, _____)
x:= ____, ______.. ____
x = y(x)=
h(x):
5. Вывод В ходе выполнения данной работы _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Числовые и степенные ряды.
1. Цель работы
1.1.Научиться вычислять члены числового ряда и исследовать числовые ряды на сходимость 1.2 Научиться раскладывать функции в ряды Тейлора и Маклорена
2. Ход работы: Вариант
1.Найдите первые три члена ряда: 2.Определить сходится или расходится данный геометрический ряд: 3.Определить сходится или расходится данный гармонический ряд: 4.Выполняется ли необходимый признак сходимости у ряда: 5.С помощью предельного признака исследовать ряд: 6.С помощью признака Даламбера исследовать сходимость ряда: 7.С помощью признака Коши исследовать сходимость ряда: 8.Исследовать на сходимость знакочередующийся ряд. Если ряд сходятся, то определить, сходятся он абсолютно или условно.
9.Разложите многочлен 10. Написать первые три, отличные от нуля, члена разложения по степеням х функции
11. Разложите функции в степенной ряд используя разложение элементарных функций и определите интервал сходимости:
a) b) c)
Заполните пропуски:
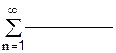
2.2.1 Дан ряд
2.2.2 Ряд вида Геометрический ряд: 1) ______________________ при 2) расходится при
2.2.3 Ряд вида
Гармонический ряд: 1) сходится при 2) _____________ при
2.2.4 Если ряд 2.2.5 Вопрос о сходимости рядов вида
2.2.6 Предельный признак сравнения. Если для положительных рядов
существует конечный
то эти ряды сходятся или расходятся ____________________.
2.2.7 Признак Даламбера. Если члены положительного ряда 2.2.8 Признак Коши. Если члены положительного ряда
2.2.9 ПризнакЛейбница. Если члены ряда
где
и их общий член стремится к ________
то ряд сходится. При этом его сумма – положительное число, меньше первого члена этого ряда.
2.2.10 Знакочередующийся ряд называется ________________________________, если сходится ряд, составленный из модулей его членов. Знакочередующийся ряд называется условно сходящимся, если он____________, а ряд, составленный из модулей его членов, _____________.
2.2.11 Ряд
называется рядом Тейлора функции
2.2.12 Если в ряде Тейлора положим
К работе допускается ______________
3. Результаты работы
Разложение функций в ряды и исследование рядов на сходимость с помощью Mathcad.
1. Цель работы
1.1 Научиться исследовать числовые ряды на сходимость с помощью пакета Mathcad; 1.2 Научиться находить радиус и область сходимости степенного ряда с помощью пакета Mathcad. 1.3 Научиться раскладывать функцию в ряд Тейлора и Маклорена с помощью пакета Mathcad.
2. Оборудование
Пакет программ MathCAD
3. Ход работы: Вариант
1. Рассматривая частичные суммы, исследовать ряд на сходимость с помощью пакета Mathcad:
2. Проверить с помощью пакета Mathcad выполнение необходимого признака сходимости у ряда:
3. Используя предельный признак сравнения исследовать ряд на сходимость с помощью пакета Mathcad:
4. Исследовать ряд на сходимость с помощью пакета Mathcad:
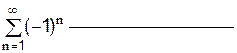
5. Исследовать на сходимость знакочередующийся ряд помощью пакета Mathcad. Если ряд сходится, то определить сходится он абсолютно или условно:
6. Найти радиус и область сходимости степенного ряда помощью пакета Mathcad:
7. Разложить функцию в ряд по степеням х помощью пакета Mathcad:
8. Разложить многочлен в ряд по степеням (х) помощью пакета Mathcad:
2.2.1 На какой панели в пакете Mathcad находятся знаки суммы и бесконечности? _____________________________________________________________________________________
2.2.2 Сделайте вывод о сходимости числового ряда, на основании исследования его частичных сумм:.
_____________________________________________________________________________________
2.2.3 Сделайте вывод о выполнении необходимого условия сходимости ряда:
_____________________________________________________________________________________
2.2.4 С каким рядом надо сравнить ряд
_____________________________________________________________________________________
2.2.5 Сделайте вывод о сходимости ряда, исследуемого по признаку Коши
2.2.6 Сделайте вывод о сходимости ряда, исследуемого по признаку Даламбера
_____________________________________________________________________________________
2.2.7 Сделайте вывод о сходимости знакочередующегося ряда:
_____________________________________________________________________________________
_____________________________________________________________________________________
2.2.9 Заполните пропуски:
К работе допускается ______________
3. Результаты работы 1)
2)
Вывод: ____________________________________________________________________________
3) α = сравним с рядом:
Вывод: ____________________________________________________________________________
4) a(n)=
Вывод: ряд _________________________________ по признаку _____________________________
5)
ряд _________________________________ по признаку _____________________________
ряд из модулей
по признаку __________________________________________________________________т.к
Вывод: _________________________________________________________________________
6)
Интервал сходимости ________________________ Сходимость на концах:
_____________________________________________________________________________________
x =
_____________________________________________________________________________________
Вывод: область сходимости: ____________________________________________________________
7) _____________________________________________________________________________________ 8) _____________________________________________________________________________________ 5. Вывод В ходе выполнения данной работы _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Приближённые вычисления с помощью рядов с использованием Mathcad и Excel.
1. Цель работы
Научиться применять ряды для приближённых вычислений значений функций и определённых интегралов
2. Оборудование
Пакет программ MathCAD, MS Excel
3. Ход работы: Вариант
1) первые двадцать членов ряда 2) найдите их модули; 3) оцените погрешность, допускаемую при замене суммы ряда суммой первых его пяти членов; 4) найдите сумму членов ряда с точностью 0,01; 5) найдите сумму членов ряда с точностью 0,001;
1) Вычислите точное значение при х =; 2) Разложите функцию в степенной ряд; 3) Замените функцию суммой первых пяти членов ряда; 4) Найдите приближённое значение функции при данном значении х; 5) Вычислите абсолютную и относительную погрешность этого приближения; 6) Постройте в одной системе координат график функции и суммы первых пяти членов ряда
1) Вычислите точное значение при х =; 2) Разложите функцию в степенной ряд; 3) Замените функцию суммой первых пяти членов ряда; 4) Найдите приближённое значение функции при данном значении х; 5) Вычислите абсолютную и относительную погрешность этого приближения; 6) Постройте в одной системе координат график функции и суммы первых пяти членов ряда
1) Вычислите точное значение; 2) Разложите подынтегральную функцию в степенной ряд; 3) Замените подынтегральную функцию суммой первых пяти членов ряда; 4) Проинтегрируйте полученное выражение; 5) 6) Вычислите абсолютную и относительную погрешность этого приближения;
3.2 Допуск к работе
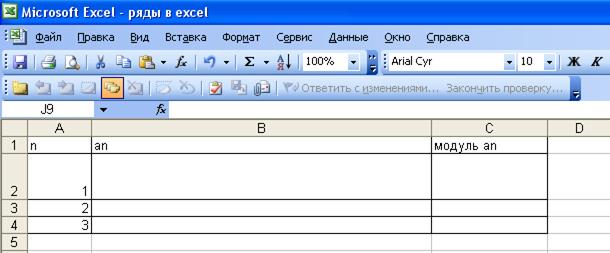
3.2.1 Заполните ячейки В2 и С2 формулами, для вычисления первых членов и их модулей для ряда:
3.2.2 Записаны первые пять членов ряда
А) Сколько членов ряда надо взять, чтобы вычислить его сумму с точностью 0,1 ____________ Б) Сколько членов ряда надо взять, чтобы вычислить его сумму с точностью 0,01 ___________ В) Какова будет погрешность, если сумму ряда заменить суммой первых его трёх членов _____
3.2.3 Как в программе Mathcad задать функцию f(x)= 3 x 2+4 sin x
____________________________________________________________________________________
3.2.4 Как в программе Mathcad разложить функцию в ряд
____________________________________________________________________________________
3.2.5
____________________________________________________________________________________
3.2.6 Точное значение 0,357, а приближённое 0,361. Запишите формулу для вычисления относительной погрешности
____________________________________________________________________________________
3.2.7 Какая кнопка в программе Mathcad вызывает шаблон для вычисления определённого интеграла?
____________________________________________________________________________________
3.2.8 Какая кнопка в программе Mathcad вызывает шаблон для нахождения неопределённого интеграла?
____________________________________________________________________________________
3.2.9 Как в программе Mathcad построить два графика в одной системе координат
____________________________________________________________________________________
К работе допускается ______________
4. Результаты работы 1)
y(x),series,___,_____ →
g(x)=
x= точное значение у(_____) = приближённое значение g(____) =
абсолютная погрешность ______ относительная погрешность ________
3) y(x) =
y(x),series,___,_____ →
g(x)=
x= точное значение у(_____) = приближённое значение g(____) =
абсолютная погрешность ______ относительная погрешность ________
4) Точное значение Подынтегральная функция g(x) =
Разложение подынтегральной функции в степенной ряд
_g(x) series, _______, →_____________________________________________________
Интеграл от полученного степенного ряда
__________________________________________________________________________
Приближённое значение интеграла
абсолютная погрешность ______ относительная погрешность ________
5) y(x) =
y(x),series,___,_____ →
члены ряда
|

 и
и 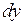
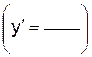
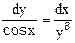 :
: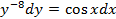 ; Б)
; Б) 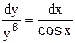 ; В)
; В) 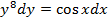 .
.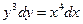 . Тогда его общее решение имеет вид:
. Тогда его общее решение имеет вид: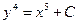 ; Б)
; Б) 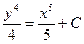 ; В)
; В) 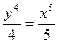 .
. Функция
Функция 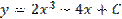 является общим решение некоторого дифференциального уравнения, тогда при
является общим решение некоторого дифференциального уравнения, тогда при 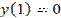 частное решение имеет вид
частное решение имеет вид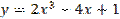 Б)
Б) 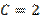
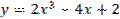 Г)
Г) 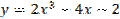
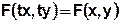
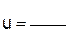 ____
____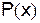 и
и 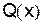 – функции переменной x или постоянные величины, называется линейным дифференциальным уравнением первого порядка, если искомая функция
– функции переменной x или постоянные величины, называется линейным дифференциальным уравнением первого порядка, если искомая функция 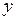 и ее производная
и ее производная 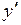 входят в это уравнение в первой степени.
входят в это уравнение в первой степени.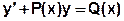 .
. , найти
, найти  и подставить эти выражения в уравнения.
и подставить эти выражения в уравнения. ппировать члены уравнения и вынести из второго и третьего слагаемых функцию
ппировать члены уравнения и вынести из второго и третьего слагаемых функцию  за скобки.
за скобки.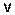 , приравняв выражение в скобках к ________ и решив полученное уравнение. При нахождении функции
, приравняв выражение в скобках к ________ и решив полученное уравнение. При нахождении функции 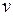 постоянная
постоянная 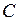 считается равной нулю.
считается равной нулю.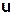 и
и  ПРАКТИЧЕСКАЯ РАБОТА 15
ПРАКТИЧЕСКАЯ РАБОТА 15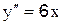
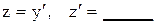
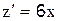

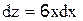
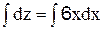





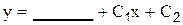
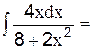

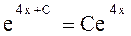

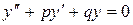
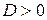
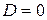
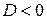
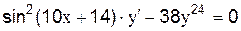
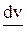
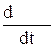
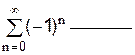 .
.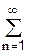
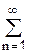
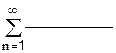
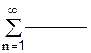 .
.
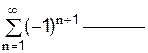
 по степеням
по степеням  .
.
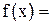
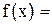
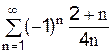 пятый член ряда:
пятый член ряда: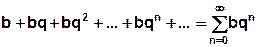 называется геометрическим рядом.
называется геометрическим рядом.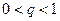 ;
; .
.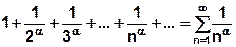 называется обобщённым гармоническим рядом.
называется обобщённым гармоническим рядом. ;
;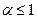 .
.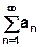 сходится, то его общий член
сходится, то его общий член 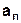 стремится к _________ т.е.
стремится к _________ т.е. 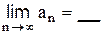 .
.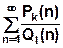 , где
, где 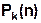 - многочлен от n степени k, a
- многочлен от n степени k, a 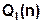 - многочлен от n степени l, полностью исчерпывается сравнением с рядом
- многочлен от n степени l, полностью исчерпывается сравнением с рядом 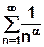 , где
, где 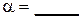 .
.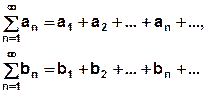
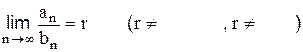
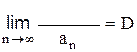 , то при
, то при  ряд сходится, а при
ряд сходится, а при  ряд расходится.
ряд расходится. , то при
, то при 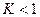 ряд _____________, а при
ряд _____________, а при 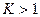 ряд _______________
ряд _______________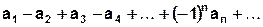 ,
,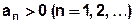 , по абсолютной величине монотонно ______________,
, по абсолютной величине монотонно ______________,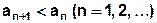
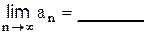 ,
,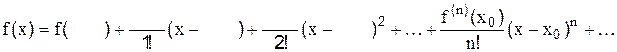
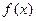 в точке
в точке 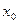 .
.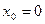 , то получим частный случай ряда Тейлора, который называют рядом Маклорена:
, то получим частный случай ряда Тейлора, который называют рядом Маклорена: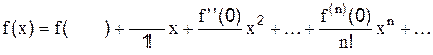 .
.

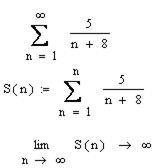
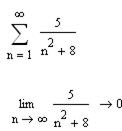
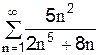 для исследования его на сходимость с использованием предельного признака сходимости?
для исследования его на сходимость с использованием предельного признака сходимости?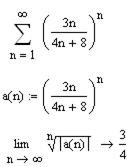


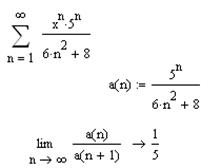
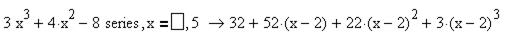
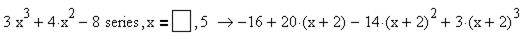
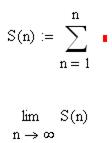
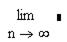
 обобщённый гармонический ряд ____________________
обобщённый гармонический ряд ____________________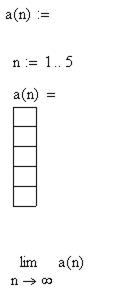
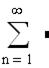
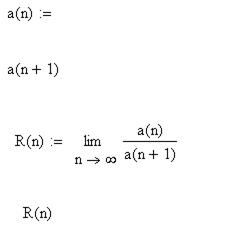
 ;
;