Алгоритм составления уравнения касательной и нормали
Согласования Рабочей программы по дисциплине «Химия» специальностей 130609-«Радиоэлектроника и связь» (по видам) 130404-«Вычислительная техника и программное обеспечение»
Подпись _____________ Дата согласования «____» ___________2015г.
Алгоритм составления уравнения касательной и нормали 1. Обозначьте абсциссу точки касания х0. 2. Вычислите □. 3. Найдите
4. Найденные значения х0, f(х0),
5. Уравнение касательной к графику функции у=f(х) в точке с абсциссой х0 имеет вид:
_________________________________________________
Уравнение нормали к графику функции у=f(х) в точке с абсциссой х0 имеет вид:
____________________________________________ 6. Выполните упрощение, полученных уравнений
К работе допускается ______________
3. Результаты работы
Частные производные .
1. Цель работы
1.1 Научиться находить частные производные функции двух переменных 1.2 Научиться находить локальные экстремумы функции двух переменных.
2. Ход работы
2.1. Вариант
Найти частные производные
1) z = ________________________
2) z = ________________________
3) Найти полный дифференциал функции z = ______________________;
4) Вычислить значения частных производных
f (x,y) = ____________________________, M0(____; ___);
5) Найти частные производные
z = ________________________
Найти вторые частные производные
6) z = ________________________
7) z = ________________________
8) Исследовать на экстремум функцию z = ________________________
9) Проверить, удовлетворяет ли указанному уравнению данная функция U.
____________________________________________________________________
2.2.1 Заполните пропуски:
А) При вычислении z’x, считают, что х – это __________, а у – постоянная (число).
Б) При вычислении z’у, считают, считают, что х – это постоянная (число),
а у – ____________________
2.2.2 Заполните таблицу
2.2.3 Вычислить значение функции
___________________________________________________________
2.2.4 Заполните таблицу:
2.2.5 Заполните таблицу:
2.2.6 Запишите формулу для вычисления полного дифференциала функции двух переменных _____________________________________________________________________________
2.2.7 Сформулируйте необходимое условие экстремума функции нескольких переменных ____________________________________________________________________________________________________________
2.2.8 Как находят r, s, t, ∆ для проверки достаточного условия экстремума функции двух переменных? _____________________________________________________________________________
2.2.9 Какими должны быть r и ∆, чтобы точка была точкой минимума? _____________________________________________________________________________
2.2.10 Каким должно быть ∆, чтобы точка не являлась точкой экстремума? _____________________________________________________________________________
К работе допускается ______________
3. Результаты работы
Решение задач дифференциального исчисления в MathCAD.
1. Цель работы
1.1. и второго порядков функций одной и нескольких переменных. 1.2. Научиться применять производную для решения геометрических физических задач с помощью пакета MathCAD.
2. Оборудование
Пакет программ MathCAD.
3. Ход работы
3.1 Вариант
1. Найти производную первого порядка
|

 и вычислите □.
и вычислите □. подставьте в уравнение касательной и нормали.
подставьте в уравнение касательной и нормали. ПРАКТИЧЕСКАЯ РАБОТА 9
ПРАКТИЧЕСКАЯ РАБОТА 9 и
и  функции
функции  .
. для данной функции
для данной функции  в точке
в точке  :
: и
и  функции
функции  .
. указанной функции. Убедиться в том, что
указанной функции. Убедиться в том, что  .
.
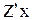

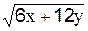
 Воспользуйтесь правилом вычисления производной частного
Воспользуйтесь правилом вычисления производной частного

 в точке M0(2;-1)
в точке M0(2;-1)




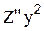


 Научиться находить с помощью пакета MathCAD производные первого
Научиться находить с помощью пакета MathCAD производные первого


