Распределение вероятности в малых выборках в зависимости
от коэффициента доверия t и объема выборки n*
* При n = ¥ в таблице даны вероятности нормального распределения. Для определения вероятности соответствующие табличные значения следует разделить на 1000.
Как видно из таблицы, при увеличении n это распределение стремится к нормальному и при n = 20 уже мало от него отличается. Покажем, как пользоваться таблицей распределения Стьюдента.
Пример 9. Предположим, что выборочное обследование 10 рабочих малого предприятия показало, что на выполнение одной из производственных операций рабочие затрачивали времени (мин.): 3,4; 4,7; 1,8; 3,9; 4,2; 3,9; 4,2; 3,9; 3,7; 3,2; 2,2; 3,9. Найдем выборочные средние затраты:
Выборочная дисперсия:
Отсюда средняя ошибка малой выборки равна:
По табл. 7.6. находим, что для коэффициента доверия t = 2 и объема малой выборки n =10 вероятность равна 0,924. Таким образом, с вероятностью 0,924 можно утверждать, что расхождение между выборкой и генеральной средними лежит в пределах от -2m до +2m, т.е. разность Глава 9. Статистическое изучение взаимосвязи социально-экономических явлений
|
n
t
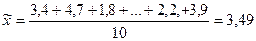мин.
.
мин.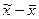
не превысит по абсолютной величине 0,56 (2´0,28). Следовательно, средние затраты времени во всей совокупности будут находится в пределах от 2,93 до 4,05 мин. Вероятность того, что это предположение в действительности неверно и ошибка по случайным причинам будет по абсолютной величине больше, чем 0,56, равна: 1-0,924 = 0,076.
