Приложение к главе 1
Таблица №1. Характеристика сингоний кристаллов.
Т аблица № 2. Характеристика различных типов решеток.
Таблица №3. Связь между индексами (hkl), величиной d и периодами решетки a, b, с для каждой сингонии.
Таблица №4. Число идентичных плоскостей P для совокупностей с разными индексами в кубической сингонии.
Глава2. Методы структурного анализа Общие положения.
Для определения В рентгенографии применяются рентгеновские лучи с длинами волн от 0,7..10-10 до 3. 10-10 м, в электронографии электроны с длинами волн де Бройля – от 3.10-12 до 6. 10-12 м, в нейтронографии – тепловые электроны с длиной волны порядка 10-10 м. По дифракционной картине можно сразу качественно судить о структуре твердого тела. Если дифракционная картина представляет набор точечных пятен (рефлексов), получающихся при рассеянии от определенных семейств атомных плоскостей (hkl), то твердое тело является монокристаллом; если дифракционная картина представляет собой набор тонких концентрических колец, то твердое тело находится в поликристаллическом состоянии; наконец, если на дифракционной картине присутствует одно, максимум два диффузных гало, то тело находится в аморфном состоянии (рис. 2.1.1, 2.1.2, 2.1.3).
2.2. Дифракция Вульфа – Брэгга. Вскоре после открытия М.Лауэ (1912) электромагнитной природы рентгеновских лучей русский ученый Ю.В. Вульф (1912) и независимо от него английские физики отец и сын Г. и Л.Брэгги дали простое истолкование интерференции рентгеновских лучей, объяснив это явление зеркальным отражением от атомных плоскостей. Пусть на кристалл, который можно представить состоящим из семейства параллельных атомных плоскостей, находящихся на одинаковом межплоскостном расстоянии d (рис 2.2.1), под углом
Отраженные от атомных плоскостей под тем же углом
Условие (2.2.1), при котором возникает интерференционный максимум, и носит название формулы Вульфа – Брэгга. Зная брэгговские углы отражения Условие дифракции в терминах обратной решетки. Рассмотрим обратную решетку и мысленно проведем атомную плоскость из семейства атомных плоскостей (hkl) c межплоскостным расстоянием d. Пусть на решетку падает излучение с волновым вектором
(2.2.2)
Умножив обе части уравнения (2.2.2) на
Уравнение (2.2.3) можно рассматривать как закон сохранения импульса для кристаллической решетки.
|

 sin
sin 
 ¹ b
¹ b
 =(h/a sinb)
=(h/a sinb) 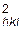 = (h/a)
= (h/a) 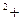 k
k  /a
/a 
 =
=  *
*




 ;
;
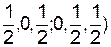

 (7)
d
(7)
d  (8)
d
(8)
d  (9)
d
(9)
d  (10)
(10)


 падает параллельный пучок монохроматических рентгеновских лучей с длиной волны
падает параллельный пучок монохроматических рентгеновских лучей с длиной волны 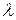 .
.
 равна целому числу n длин волн
равна целому числу n длин волн 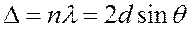 или
или  . (2.2.1)
. (2.2.1)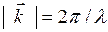 и выполняется условие дифракции Вульфа-Брэгга (2.2.1). Тогда из рис.2.2.1 и ранее доказанной теоремы,
и выполняется условие дифракции Вульфа-Брэгга (2.2.1). Тогда из рис.2.2.1 и ранее доказанной теоремы,  устанавливающей связь между семейством атомных плоскостей и вектором обратной решетки, можно записать следующую цепочку равенств:
устанавливающей связь между семейством атомных плоскостей и вектором обратной решетки, можно записать следующую цепочку равенств:
 где m – порядок дифракционного максимума. При m=1 условие дифракционного максимума принимает окончательный вид
где m – порядок дифракционного максимума. При m=1 условие дифракционного максимума принимает окончательный вид получим
получим