Обратная решетка
Для идеального бесконечного монокристалла обратная решетка представляет бесконечное трехмерное распределение точек, расстояние между которыми обратно пропорционально расстояниям между плоскостями прямой решетки. Размерность радиуса-вектора обратной решетки [м-1]. Эта размерность совпадает с размерностью волнового вектора Множество волновых векторов
Обратная решетка всегда определяется по отношению к прямой решетке. Пусть
Докажем, что обратная решетка, построенная на этих векторах также является трансляционной. Легко показать, что
, где Запишем линейную комбинацию из основных векторов обратной решетки
где m1, m2,m3 - любые числа. Найдем скалярное произведение векторов
Если К - вектор обратной решетки, то выполняется равенство
Таким образом, если в выражении (1.7.5) m1, m2,m3 - целые числа, вектор Атомная плоскость решетки Бравэ – любая плоскость, содержащая, по меньшей мере, 3, не лежащих на одной прямой, узла. Семейство атомных плоскостей – множество параллельных, равноотстоящих друг от друга атомных плоскостей, которые в своей совокупности содержат все узлы трехмерной решетки Бравэ. Каждая атомная плоскость является плоскостью какого-либо семейства. Понятие обратная решетка позволяет классифицировать различные семейства атомных плоскостей и очень удобно для структурного анализа. Такая квалификация основана на теореме, устанавливающей связь между семейством атомных плоскостей и вектором обратной решетки: для всякого семейства атомных плоскостей, отстоящих друг от друга на расстоянии d, существуют такие векторы обратной решетки, которые перпендикулярны к этим плоскостям, а наименьший из них имеет длину равную 2 Докажем эту теорему. Пусть имеется семейство атомных плоскостей, отстоящих друг от друга на расстоянии d. Направим плоскую волну: exp[i(
|

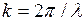 . Поэтому множеству радиус-векторов обратной решетки можно сопоставить множество плоских волн. Тогда точное определение обратной решетки можно сформулировать следующим образом:
. Поэтому множеству радиус-векторов обратной решетки можно сопоставить множество плоских волн. Тогда точное определение обратной решетки можно сформулировать следующим образом: образуют обратную решетку по отношению к прямой решетке Бравэ с вектором трансляции
образуют обратную решетку по отношению к прямой решетке Бравэ с вектором трансляции 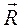 , если плоские волны с волновыми векторами
, если плоские волны с волновыми векторами  имеют периодичность данной решетки Бравэ, т.е.
имеют периодичность данной решетки Бравэ, т.е. или
или 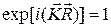 (1.7.1)
(1.7.1) - основные векторы прямой решетки, тогда обратную решетку порождают три основных вектора следующим образом:
- основные векторы прямой решетки, тогда обратную решетку порождают три основных вектора следующим образом: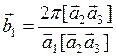 ,
, 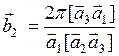 ,
,  . (1.7.2)
. (1.7.2) , (1.7.3)
, (1.7.3)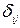 - символ Кронекера.
- символ Кронекера.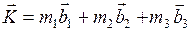 , (1.7.4)
, (1.7.4)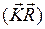 . Получим
. Получим
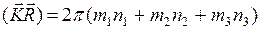 (1.7.5)
(1.7.5)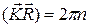 , где n целое число. Выражение в скобках в формуле (1.7.5) может быть целым при любых целых n1, n2,n3 только если m1, m2,m3 также целые числа.
, где n целое число. Выражение в скобках в формуле (1.7.5) может быть целым при любых целых n1, n2,n3 только если m1, m2,m3 также целые числа.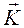 является вектором трансляции, а обратная решетка, порожденная этим вектором, также является трансляционной.
является вектором трансляции, а обратная решетка, порожденная этим вектором, также является трансляционной. /d.
/d.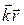 )] с волновым вектором k=2
)] с волновым вектором k=2 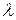 , выбранная нами плоская волна будет иметь одинаковое значение фазы на всех атомных плоскостях. Возьмем любой узел на любой атомной плоскости и примем его за начало координат. Тогда
, выбранная нами плоская волна будет иметь одинаковое значение фазы на всех атомных плоскостях. Возьмем любой узел на любой атомной плоскости и примем его за начало координат. Тогда  и вектор
и вектор 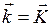 , что и требовалось доказать.
, что и требовалось доказать.


