Лабораторная работа №15
Тема: Система одновременных уравнений Содержание занятия. 1. Применение косвенного метода наименьших квадратов. 2. Применение ДМНК к простейшей сверхидентифицируемой модели. Литература: [1] стр200-204,[2] стр113-115, [8] стр30-341
Задание Пусть для построения данной модели мы располагаем некоторой информацией по 5 регионам:
Построить структурную эконометрическую модель, применив косвенный метод наименьших квадратов и двухшаговый метод наименьших квадратов. Методические указания по выполнению задания: Приведенная форма модели составит: Для каждого уравнения приведенной формы модели применяем традиционный МНК и определяем
Применительно к рассматриваемому примеру, используя отклонения от средних уровней, имеем: у1=0,852х1+0,373х2 Аналогично применяем МНК для второго уравнения приведенной формы модели. Система нормальных уравнений составит: Откуда второе уравнение приведенное уравнение составит: у2=-0,072х1-0,00557х2 Таким образом, приведенная форма модели имеет вид: Переходим от приведенной формы к структурной форме модели, т.е. к системе уравнений: Для этой цели из первого уравнения приведенной формы модели надо исключить х2 выразив его из второго уравнения приведенной формы и подставив в первое:
Чтобы найти второе уравнение структурной модели обратимся вновь к приведенной форме модели. Из второго уравнения приведенной формы модели следует исключить х1, выразив его через первое уравнение и подставив во второе: Итак, структурная форма модели имеет вид: Применим двухшаговый метод наименьших квадратов к простейшей сверхидентифицируемой модели: На основе второго уравнения данной системы найдем теоретические значения для эндогенной переменной Расчетные данные для второго шага ДМНК.
Заменяя фактические значения Таким образом, сверхидентифицируемое структурное уравнение составит
8. Материалы для самостоятельной работы обучающегося: Тема: Сведения из теории вероятности и математической статистики Задача №1 Законы распределения независимых случайных величин Х и Y приведены в таблицах
Найти дисперсию и среднее квадратическое отклонение случайной величины Z=2X+3Y. Задача №2 Дан ряд распределения случайной величины Х:
Необходимо: 1) найти математическое ожидание, дисперсию, среднее квадратическое отклонение, коэффициент вариации; 2) определить функцию распределения F(x) и построить ее график; 3) найти вероятность попадания случайной величины в интервал [0,2 ] Задача №3 Предприятие имеет 5 станков по производству камня, работающих независимо друг от друга. Вероятность отказа любого из них p=0,25. Определите параметры закона биномиального распределения случайной величины- числа отказа станков. Задача №4 Определите вероятность невыхода специалиста на работу по причине болезни, если среднее число заболевших специалистов составляет 4 человека. Задача №5 Какова вероятность того, что при 100-кратном бросании монеты число выпадений герба будет от 45 до 55?
Тема: Проверка статистических гипотез Задача №1 Производитель утверждает, что доля бракованных изделий не превосходит 3%. В случайной выборке объема п =100 изделий оказалось 5 бракованных изделий. Не противоречит ли это утверждению производителя? Доверительная вероятность р =95%. Задача №2 Производственная линия выпускала 5% бракованных товаров. Было предложено усовершенствование, призванное снизить процент брака. После переналадки линии на осмотр поступило 300 единиц товара, из которых бракованными оказались 9 единиц. Можно ли на 1% уровне значимости считать, что качество продукции производственной линии улучшилось? Задача №3 Инвестиция 1 рассчитана на п1 =14 лет, дисперсия ежегодных прибылей Задача №4 Урна содержит большое количество белых и черных шаров. 100 раз производится следующее действие: из урны наугад достается шар, фиксируется его цвет, затем шар опускается обратно в урну, после чего шары перемешиваются. Оказалось, что 67 раз достали белый шар, 33 раза – черный. Можно ли на 5% уровне значимости принять гипотезу о том, что доля белых шаров в урне составляет 0,6?
Тема: Парная линейная регрессия и корреляция. Задача №1 Имеются следующие данные об уровне механизации работ Х(%) и производительности труда Y(т/ч) для 14 однотипных предприятий:
Необходимо: 1)оценить тесноту связи и направление связи между переменными с помощью коэффициента корреляции; 2) найти уравнение регрессии Y по Х; 3) найти коэффициент детерминации и пояснить его смысл; 4) проверить значимость уравнения регрессии на 5%-м уровне; 5) построить 95%-й доверительные интервалы для каждого из параметров уравнения регрессии. Задача №2 По данным 30 нефтяных компаний получено следующее уравнение регрессии между оценкой Y (ден. ед.) и фактической стоимостью Х (ден. ед.) этих компаний: ух=0,875х+295. Найти: 95%-е доверительные интервалы для среднего и индивидуального значений оценки предприятий, фактическая стоимость которых составила 1300 ден.ед., если коэффициент корреляции между ними равен 0,76, а среднее квадратическое отклонение переменной Х равно 270 ден.ед.
Тема: Модель множественной линейной регрессии. Задача №1 По 30 наблюдениям получены следующие данные:
1.Найти скорректированный коэффициент корреляции, оцените значимость уравнения регрессии в целом. 2. Определите частные коэффициенты эластичности. 3. Оцените параметр а. Задача №2 По 50 семьям изучалось потребление мяса – у (кг на душу населения) от дохода - х1 (д.ед. на одного члена семьи) и от потребления рыбы – х2 (кг на душу населения). Результаты оказались следующими:
1.Используя t–критерий Стьюдента, оцените значимость параметров уравнения. 2.Рассчитайте F–критерий Фишера. 3. Оцените по частным F–критериям Фишера целесообразность включения в модель: а) фактора х1 после фактора х2; б) фактора х2 после фактора х1. Тема: Фиктивные переменные Задача №1 Необходимо исследовать зависимость между результатами письменных вступительных и и курсовых (на 1 курсе) экзаменов по математике. Получены следующие данные о числе решенных задач на вступительных экзаменах Х (задание - 10 задач) и курсовых экзаменах Y (задание – 7 задач) 12 студентов, а также распределение этих студентов по фактору «пол»
Построить линейную регрессионную модель Y по Х с использованием фиктивной переменной по фактору «пол». Можно ли считать, что эта модель одна и та же для юношей и девушек? Тема: Нелинейные эконометрические модели. Задача №1 Для трех видов продукции А, В, С модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом: уА=600, уВ=80+0,7х, уС=40х0,5 . 1.Определите коэффициенты эластичности по каждому виду продукции и поясните их смысл. 2. Сравните при х=1000 эластичность затрат для продукции В и С. 3.Определите, каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности продукции В и С были равны. Задача №2 Зависимость объема производства у (тыс.ед.) от численности занятых х (чел.) по 15 заводам концерна характеризуется следующим образом: Определите: 1. Индекс корреляции. 2. Значимость уравнения регрессии. 3. Коэффициент эластичности, предполагая, что численность занятых составляет 30 человек. Задача №3 Зависимость среднемесячной производительности труда от возраста рабочих характеризуется моделью:
Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера. Тема: Гетероскедастичность Задача №1 В таблице приведены данные по 18 наблюдениям модели пространственной выборки:
Предполагая, что ошибки регрессии представляют собой нормально распределенные случайные величины, проверить гипотезу о гомоскедастичности, используя тест Голдфелда-Квандта. Задача №2 При оценивании модели пространственной выборки обычным методом наименьших квадратов получено уравнение: Тема: Динамический ряд. Задача №1 Имеются данные об урожайности зерновых в хозяйствах области:
1. Обоснуйте выбор уравнения тренда и определите его параметры. 2. Дайте прогноз урожайности зерновых на следующий год. Задача №2 По данным за 30 месяцев некоторого временного ряда хt были получены значения коэффициентов автокорреляции уровней: r1=0,63; r2=0,38; r3=0,72; r4=0,97; r5=0,55; r6=0,40; r7=0,65. Требуется: 1.Охарактеризовать структуру этого ряда, используя графическое изображение. 2. Для прогнозирования значений хt в будущие периоды предполагается построить уравнение авторегрессии. Выбрать наилучшее уравнение, обосновать выбор. Указать общий вид этого уравнения. Задача №3 В таблице приводятся данные об уровне дивидендов, выплачиваемых по обыкновенным акциям (в процентах), и среднегодовой стоимости основных фондов компании (Х, млн. ден. ед.) за последние девять лет.
1.Определите параметры уравнения регрессии по первым разностям и дайте их интерпретацию. В качестве зависимой переменной используйте показатель дивидендов по обыкновенным акциям. 2. В чем состоит причина построения уравнения регрессии по первым разностям, а не по исходным уровням рядов? Тема: Система одновременных уравнений Задача №1 Имеется следующая гипотетическая модель: Приведенная форма исходной модели имеет вид: 1. Проверьте структурную форму модели на идентификацию. 2. Определите структурные коэффициенты модели. Задача №2 1.Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели. 2.Определите метод оценки параметров модели. 3. Запишите приведенную форму модели. Модель Кейнса (одна из версий): где C – потребление; Y –ВВП; I – валовые инвестиции; G – государственные расходы; t – текущий период; t-1- предыдущий период.
Тематика рефератов по дисциплине «Эконометрика» История возникновения эконометрики Жизнь и деятельность ученых, внесших вклад в развитие эконометрики Виды эконометрических моделей. Экономические данные. Виды и их свойства Законы распределения случайных величин. Нормальное распределение и его применение в экономических расчетах. Проверка статистических гипотез. Проблемы спецификации эконометрических моделей. Определение мультиколлинеарности и методы устранения мультиколлинеарности. Фиктивные переменные и их сущность Нелинейные модели регрессии. Производственные функции. Гомоскедастичность и гетероскедастичность остатков. Тесты для оценки гетероскедастичности Ранговая корреляция. Частная корреляция. Ложная корреляция. Обобщенный метод наименьших квадратов. Трехшаговый метод наименьших квадратов. Прогнозирование на основе временных рядов. Автокорреляция остатков временного ряда. Тесты на наличие автокорреляции. Методы устранения автокорреляции Динамические эконометрические модели Методы отбора факторов для построения регрессии Статистика Дарбина-Уотсона и ее применение Эконометрическое моделирование в маркетинговых исследованиях. Модель адаптивных ожиданий. Модели с распределенным лагом. 30 Оценивание параметров моделей с распределенным лагом.
10. Методические указания по прохождению учебной, производственной и преддипломных практик, формы отчетной документации (если требует специфика дисциплины)
|


 -коэффициенты. Чтобы упростить процедуру расчетов, можно работать с отклонениями от средних уровней, т.е.
-коэффициенты. Чтобы упростить процедуру расчетов, можно работать с отклонениями от средних уровней, т.е.  . Тогда для первого уравнения приведенной формы модели система нормальных уравнений составит:
. Тогда для первого уравнения приведенной формы модели система нормальных уравнений составит:












 . Решая данную систему, получим следующее первое уравнение приведенной формы модели:
. Решая данную систему, получим следующее первое уравнение приведенной формы модели: Применительно к нашему примеру имеем:
Применительно к нашему примеру имеем: 
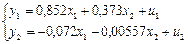

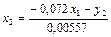 . Тогда
. Тогда 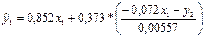
 - первое уравнение структурной модели.
- первое уравнение структурной модели. и
и 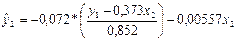 .
.  - второе уравнение структурной модели.
- второе уравнение структурной модели.
 . Используем те же исходные данные, поэтому получим ту же систему приведенных уравнений:
. Используем те же исходные данные, поэтому получим ту же систему приведенных уравнений: 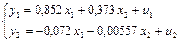
 . С это целью во второе уравнение подставляем значения
. С это целью во второе уравнение подставляем значения 
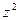

 е.е.
е.е.  . Откуда
. Откуда  .
. . Ввиду того, что второе уравнение системы не изменилось, то его структурная форма, найденная из системы приведенных уравнений та же:
. Ввиду того, что второе уравнение системы не изменилось, то его структурная форма, найденная из системы приведенных уравнений та же: 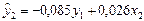 . В целом рассматриваемая система одновременных уравнений составит:
. В целом рассматриваемая система одновременных уравнений составит:
 =(15%)2. Инвестиция 2 рассчитана на п2 =12 лет, дисперсия ежегодных прибылей
=(15%)2. Инвестиция 2 рассчитана на п2 =12 лет, дисперсия ежегодных прибылей  =(20%)2. Предполагается, что распределение ежегодных прибылей на инвестиции подчиняется нормальному закону распределения. Равны ли риски инвестиций 1 и 2? Доверительная вероятность р =99%.
=(20%)2. Предполагается, что распределение ежегодных прибылей на инвестиции подчиняется нормальному закону распределения. Равны ли риски инвестиций 1 и 2? Доверительная вероятность р =99%.
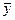




 . Доля остаточной дисперсии в общей 20%.
. Доля остаточной дисперсии в общей 20%. . Ее использование привело к следующим результатам:
. Ее использование привело к следующим результатам:
 .Уравнение регрессии квадратов остатков на квадраты регрессоров имеет вид:
.Уравнение регрессии квадратов остатков на квадраты регрессоров имеет вид:  . Зная, что объем пространственной выборки п=200, проверить гипотезу Уайта о гомоскедастичности модели.
. Зная, что объем пространственной выборки п=200, проверить гипотезу Уайта о гомоскедастичности модели.





