Лабораторная работа №12

Тема: Динамический ряд.

Содержание занятия.

1.Построение аддитивной и мультипликативной моделей временного ряда.

2.Прогнозирование по аддитивной и мультипликативной моделям.

Литература: [1] стр239-255,[2] стр137

Задание Пусть имеются поквартальные данные о прибыли компании за 3 года.

Год	Квартал
I	II	III	IV

Построить мультипликативную модель временного ряда и сделать прогноз на последующие два квартала.

Методические указания по выполнению задания:

Для построения мультипликативной модели временного ряда необходимо:

1) Провести выравнивание временного ряда методом скользящей средней.

2) Найти оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (графа 5).

Расчет оценок сезонной компоненты в мультипликативной модели

№ квартала, t	Прибыль, Yt	Скользящая средняя за 4 квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
		- 81,5 81,0 79,0 76,5 75,0 73,0 70,0 67,0 64,5 - -	- - 81,25 80,00 77,75 75,75 74,00 71,50 68,50 65,75 - -	- - 1,108 0,800 0,900 1,215 1,081 0,811 0,905 1,217 - -

Найденные оценки используются для расчета сезонной компоненты S. Для этого находятся средние за каждый квартал оценки сезонной компоненты Si. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле (в примере равно 4).

Расчет сезонной компоненты

Показатели	Год	№ квартала
I	II	III	IV
		- 0,900 0,905	- 1,215 1,217	1,108 1,081 -	0,800 0,811 -
Итого за квартал		1,805	2,432	2,189	1,611
Средняя оценка сезонной компоненты		0,9025	1,216	1,0945	0,8055
Скорректированная сезонная компонента, Si		0,8983	1,2104	1,0895	0,8018

Имеем: 0,9025+1,216+1,0945+0,8055=4,0185.

Определим корректирующий коэффициент: k= 4:4,0185=0,9954. Определим скорректированные значения сезонной компоненты, умножив её средние оценки на корректирующий коэффициент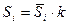

3) Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Получим величины T*E=Yt/Si, которые содержат только тенденцию и случайную компоненту.

Расчет выравненных значений Т и ошибок в мультипликативной модели

t	Yt	Si	T*E=Yt/Si	T	T*S	E=Yt-(T*S)	E2
		0,8983 1,2104 1,0895 0,8018 0,8983 1,2104 1,0895 0,8018 0,8983 0,2104 1,0895 0,8018	80,15 82,62 82,61 79,92 77,92 76,01 73,43 72,34 69,02 66,09 62,41 59,86	94,94 82,87 80,79 78,71 76,64 74,56 72,48 70,41 68,33 66,25 64,17 62,10	0,943 0,996 1,022 1,014 1,016 1,019 1,013 1,027 1,010 0,997 0,972 0,964	-4,306 -0,304 1,977 0,886 1,155 1,749 1,026 1,546 0,617 -0,195 -1,923 -1,793	18,545 0,092 3,908 0,784 1,334 3,062 1,054 2,390 0,381 0,038 3,698 3,217

4) Определить компоненту Т. Для этого рассчитываются параметры линейного тренда, используя уровни (Т*Е). Уравнение тренда имеет следующий вид: Т=87,022-2,076t. Подставляя в это уравнение значения t=1,2,…12 найти уровни Т для каждого момента времени.

5) Найти уровни временного ряда, умножив уровни Т на значения сезонной компоненты для соответствующих кварталов.

6) Расчет ошибки в мультипликативной модели производится по формуле E=Yt-(T*S) (графа 7).

Пусть необходимо дать прогноз прибыли в течение первого полугодия следующего года. Прогнозное значение F_t уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компоненты. Для определения трендовой компоненты следует воспользоваться уравнением тренда Т=87,022-2,076t.

Т₁₃=87,022-2,076*13=60,034.

Т₁₄=87,022-2,076*14=57,958.

Значения сезонной компоненты S₁=0,8983; S₂=1,2104.

F₁₃= Т₁₃* S₁=60,034*0,8983=53,928

F₁₄= Т₁₄* S₂=57,958*1,2104=70,152

Прогноз ожидаемой прибыли компании на первое полугодие составит: 53,928+70,152=124,080 тыс. у.ед.