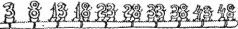Старый знакомый

(Таня – Нулику)

 

Дорогой Нулик! Мы все еще в том же заколдованном месте.

Расшифровали записку и стали решать задачу стручка. Бились, бились – ничего не выходит! Хотели уж идти в Автоматическую справочную, но Пэ отсоветовал.

– Если вы в самом деле хотите помочь одному незнакомцу, – сказал он таинственно, – решите эту задачу сами. Но для этого необходимо составить уравнение…

Легко сказать, составить уравнение! Составить треугольник Паскаля – это еще куда ни шло, но уравнение?…

– Понимаю, – посочувствовал Пэ, – вы еще не были на нашем образцовом строительстве. Иначе вы уже знали бы, с чем это едят.

– Строительство и уравнение? – покачал головой Сева.

– Ничего удивительного! Неужели вы думаете, что можно построить что‑нибудь без уравнений?

Мы хотели сейчас же, сию минуту отправиться на это необыкновенное строительство, но директор напомнил, что сегодня праздник. Придется подождать до завтра.

– Кстати, – добавил он, – сейчас в нашем кафе начнется выступление знаменитого фокусника. Хотите посмотреть?

Не стоило и спрашивать. Кто же откажется от такого удовольствия? И можешь себе представить, на эстраде появился тот самый фокусник, который выступал в карликанском цирке! Мы обрадовались ему, как родному. Сейчас он станет делить нуль на тысячу частей, покажет Великана из Бесконечности… Но все было иначе.

Фокусник поднял руку, и в ней неизвестно откуда появилась длинная палка. Потом он выпустил палку, но она не упала, а продолжала лежать в воздухе, как на столе. Фокусник предложил публике убедиться, что палка не какая‑нибудь фальшивая, а выточенная из цельного куска дерева.

Первым на эстраду выскочил Сева, за ним – еще несколько посетителей. Все они подтвердили, что никакого обмана нет.

Тогда фокусник взмахнул рукой, и вот уже на палке, как воробьи на проводах, уселись его ассистенты‑числа.

– Обратите внимание, – сказал фокусник, – числа расположены на палке в определенном порядке. Каждое, начиная слева, больше предыдущего на одно и то же число.

– На два! – крикнули из зала.

– Правильно, на два.

Фокусник снова взмахнул рукой, и на палке появились другие числа:

– Попрошу уважаемую публику ответить: какой порядок в этом ряду чисел?

– Каждое число больше предыдущего на пять, – сказала я.

– Благодарю вас, – поклонился фокусник. – Так вот, должен вам сделать потрясающее сообщение: ряд чисел, где каждое последующее число больше предыдущего на постоянную величину, называется ар‑р‑р‑ифметической пр‑р‑р‑ро‑грессией. Но это еще не все. Эта постоянная величина называется разностью прогрессии. И более того: сами числа называются членами прогрессии!

– Ага! Значит, в первом случае разность прогрессии была равна двум, а во втором – пяти, – сказал кто‑то.

– Браво! – воскликнул фокусник.

Сева толкнул меня локтем:

– Все это хорошо, но когда начнутся фокусы?

Фокусник, наверное, услышал его слова. Он лукаво посмотрел на Севу и снова взмахнул рукой. И вдруг палка, толстая палка, выточенная из цельного куска дерева, согнулась посредине и концы ее сошлись. Теперь числа, сидевшие, на равном расстоянии от концов, оказались точно друг против друга: три – против сорока восьми, восемь – против сорока трех, и так далее.

– Попрошу сложить любую пару чисел, – предложил фокусник.

Мы сложили: три и сорок восемь. Получилось пятьдесят один. Затем восемь и сорок три. Снова пятьдесят один. Тринадцать плюс тридцать восемь… Что такое? Опять пятьдесят один! И восемнадцать плюс тридцать три, и двадцать три плюс двадцать восемь – все они в сумме давали одно и то же число: пятьдесят один.

– Вот это уже фокус! – закричал Сева.

– Где фокус? – развел руками фокусник. – Это вы называете фокусом? Ха‑ха‑ха! Обыкновеннейшее алгебраическое правило.

– Но в чем же тогда фокус? – хорохорился Сева.

Фокусник небрежно разогнул палку, словно она была из бумаги.

– Попробуйте положить палку в воздухе, согнуть ее пополам, потом снова разогнуть и вы не станете задавать мне такие вопросы!

Все засмеялись, захлопали, а фокусник продолжал: – Предлагаю сделать небольшой опыт. Кто из вас быстрее сложит все числа этой арифметической прогрессии? Раз, два, три – начали!

В зале зашептались, зашуршала бумага, задвигались карандаши. Мы тоже стали складывать:

3 + 8 + 13 + 18 + 23 + 28 + 33 + 38 + 43 + 48.

Сначала складывали в уме, потом – столбиком. От волнения все время сбивались. Нам очень хотелось сосчитать быстрее. Но почему‑то получалось медленно. Под конец чуть не подрались.

Но тут фокусник поднял руку:

– Стоп! Никуда не годится, слишком долго считаете. Можно гораздо быстрее. – И он снова согнул палку пополам. – Попрошу убедиться! Перед вами пять пар чисел. Сумма каждой – пятьдесят один, а сумма пяти пар в пять раз больше. Беру пятьдесят один, умножаю на пять. И что я получаю? Я получаю двести пятьдесят пять! А теперь попробуйте сами. Желающие, проходите, проходите, не стесняйтесь!

Мне уж давно хотелось принять участие в опытах, да как‑то неловко было. Но Олег подтолкнул меня, и я очутилась на эстраде.

Теперь на палке были уже другие числа:

– Прошу найти сумму этих чисел, – сказал фокусник. – Быстренько, быстренько!

– В прогрессии восемь членов, – сказала я, – значит, четыре пары. Сумма крайних членов – сорок два. Умножаю сорок два на четыре. Получается сто шестьдесят восемь. Правильно?

– Абсолютно правильно! – подтвердил фокусник. – Сто шестьдесят восемь!

– Но позвольте, – вмешался Сева, – почему вы в Аль‑Джебре решаете карликанские задачи? Это же простая арифметика!

– Вот именно простая. Применяя такой способ, мы упрощаем решение. Обратите внимание: упрощение – один из главных девизов Аль‑Джебры. Другой ее девиз – обобщение. Правило, которое я сейчас вам показал, справедливо для любой арифметической прогрессии. И следовательно…

– Следовательно, его можно выразить буквами, – перебил Олег.

– Великолепно! – воскликнул фокусник. – Вы попали в самую точку. Итак, размещаю на палке не числа, а буквы. Каждый член прогрессии обозначаю буквой а и снабжаю ее порядковым числом, чтобы не было никакой путаницы. Такое число называется индексом и ставится чуть ниже и справа от буквы.

Фокусник подал знак, и буквы а в сопровождении индексов быстро расселись на палке:

– Внимание! Приступаю к выводу формулы. В этом ряду под а и а можно подразумевать любые числа.

– Ну конечно, – сказал Сева, – так же как и под всеми остальными.

– Думайте, думайте, молодой человек! – возразил фокусник. – Ведь все эти а – члены одной арифметической прогрессии. Поэтому произвольно могут быть взяты только первые два а. Величины остальных зависят от разности между двумя первыми. Итак, обозначаю разность буквой d. Ведь разность прогрессии постоянна. Тогда a = а + d; а = а + d; a = a + d.

И так до конца прогрессии. Понятно?

– Понятно, понятно! – закричали все.

– Продолжаю! Надеюсь, все заметили, что в этой прогрессии восемь членов. Или четыре пары. Сумму крайних членов записываю так: а + а.

Обозначаю сумму всех членов большой латинской буквой Эс – S. Ведь слово «сумма» начинается с этой буквы! Значит, S = 4(а + a).

Кто‑то спросил:

– А если в прогрессии десять членов? Как тогда вычислить сумму?

– Точно так же, – ответил фокусник. – Только пар станет уже не четыре, а пять, и последний член прогрессии будет a: S = 5 (a + a).

– Стало быть, это справедливо для любого числа членов? – не унимался дотошный зритель.

– Какое число членов вам угодно сложить?

– Пять! Двадцать! Сто семьдесят пять! Двести сорок! Миллион семьсот тысяч! – неслось со всех сторон.

Фокусник закрыл уши руками:

– Тише, тише! Сейчас все ваши просьбы будут исполнены.

Он подождал, когда все успокоятся, и снова заговорил:

– Обозначаю число членов буквой Эн – n. Тогда последний член прогрессии будет а энное – a, а сумма крайних членов a + a.

Нетрудно догадаться, что число пар будет в два раза меньше числа n, то есть n/2. Вот и выходит, что сумма членов запишется так: S = (a + a) * n/2.

– Разрешите спросить, – сказал Олег, – если число членов прогрессии нечетное, как вы его разобьете на пары?

– А уж над этим вы подумайте сами. Но поверьте честному слову фокусника – формула нисколько не изменится.

Он еще раз сложил свою палку, и она тут же исчезла. Все захлопали, засмеялись. Фокусник тоже сложился пополам и исчез так же неожиданно, как его палка.

Вот какие фокусы показывают в Аль‑Джебре.

Таня.