Взаимозаменяемость ресурсов в задачах линейного программирования
Пусть мы находимся в классе задач линейного программирования:
Yi = bi - å aij × xj0 cj, aij, bi – параметры модели xj0 – оптимальное решение yi – запасы ресурса i –го вида Ф(х0), Y(х0) – выходные характеристики данной модели (результат решения оптимизационной задачи). Реальная жизнь, рыночная обстановка всегда сопровождаются определенными возмущениями (это различные изменения). ∆cj – отклонение по коэффициентам целевой функции, ∆aij – отклонение по нормативам затрат, ∆bi – отклонение по ресурсу. Предположим, что в системе возникло возмущение по некоему ресурсу Dbs. Dbs Þ Dхj j-тая продукция имеет особо важное значение для системы. Ее выпуск необходимо сохранить на прежнем уровне, т.е. Dхj = 0. Dхj = ajs Dbs В этом случае можно сформулировать задачу взаимозаменяемости ресурсов. aj > 0; Dbs < 0 Þ Dхj < 0. Однако есть некоторый ресурс bl, которым мы можем управлять. ajl > 0 c изменением запасов ресурсов bl. Надо рассчитать дополнительное количество l – ресурса, которое позволило бы компенсировать недопоставку ресурса S. Dхj = ajl Dbl Dхj = 0 ajs Dbs = - ajl Dbl – условие взаимной компенсации Dbl = - (aj Dbs)/ ajl - коэффициент взаимозаменяемости Введем в рассмотрение характеристику чувствительности критерия (целевой функции) к вариациям запаса ресурсов. ¶Ф
¶bi
Ф = å Сjхj Dхj
¶bi D Ф = Zi Dbi D Ф = å Zs Dbs s Коэффициенты Zi для дефицитных ресурсов всегда больше 0. для недефицитных ресурсов коэффициенты Zi равны 0.
|

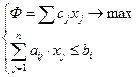

 Zi = i = 1, n
Zi = i = 1, n Zi =å Сj =å Сjaji
Zi =å Сj =å Сjaji 


