Неопределенность в активных системах.
Пусть мы находимся в классе задач нелинейного программирования:
i=1 2ri n å хi = R i=1 хi – объем производства каждого предприятия, ri – показатель эффективности работы i-того предприятия. R – в таком количестве система должна произвести продукцию. Ф-суммарные затраты В реальных условиях решение приходится принимать в условиях, когда информация о параметре ri отсутствует. Не обладая достоверной информацией, центр имеет представление об области допустимых состояний параметра: di ≤ ri ≤ Di.Чем больше эта область, тем хуже, тем выше степень неопределенности. Неопределенность надо устранять. Методы снятия неопределенности: 1) Метод гарантированного результата- центр исходит из наихудшей для себя гипотезы и руководствуясь этим принимает решение. Параметры системы, по кот. имеется неопределенность, дифференцируются на «хорошие» и «плохие». Хорошие – их рост способствует росту критерия определенности. Рост плохих приводит к уменьшению критерия определенности. Достоинство: метод понятен и легок в исполнении, доступен Недостаток: метод приводит к недополучению возможной полезности, т.е. не эффективный 2) Метод статистического моделирования. Идея метода заключается в следующем: центр не имеет достоверной информации о значениях параметров на будущие периоды. Однако, он располагает ретро информацией о значениях этих параметров. Эти методы применимы только в случаях, когда медленно развиваются процессы. 3)Метод формирования данных. Центр полагает, что есть какие-либо реальные значения, о кот. ему точно неизвестно. Но сущ-т предел (диапазон), в кот. колеблются значения показателя эфф-ти. Центр открывает возможность перед элементами проявить активность, принимает заявки и формирует свою целевую функцию. План, кот. получает элемент, пропорционален его оценке, и зависит не только от его собственной оценки, но и от совокупности оценок, кот. дали др. элементы. Достоинство: это есть путь снятия неопределенности в принятии решений Недостаток: здесь присутствует сознательное искажение, т.е. Центру трудно добиться достоверной информации. 12.Метод гарантированного результата. Центр планирует производственное задание для однотипных предприятий. Исходим из того, что система в целом должна произвести R продукции. Задача центра найти плановое задание по объему производства каждому i-му производственному элементу. При этом центр стремиться минимизировать общие затраты, которые будут иметь место при реализации задания. xi-план. задание по объёму выпускаемой продукции каждому i-му элементу.
13. Методы прогнозирования при снятии неопределённости. Будем рассматривать прогнозирование, основываясь на статистическом моделировании. Метод статистического моделирования подразумевает, что ЛПР не имеет достоверной информации о значениях параметров на будущий период. Но ЛПР располагает ретроинформацией о значениях этих параметров.
t0 t
Выдвинем гипотезу: имеется ретроинформация и в ней прослеживается некая линейная зависимость rм = α + βt.(а-значение r в t=0, в-показывает насколько изменится r при изменении t на 1. Для оценки погрешности модели вводится понятие дисперсия:
14. Метод формирования данных в активных системах. Исходим из того, что система в целом должна произвести R продукции. При этом центр стремиться минимизировать общие затраты, которые будут иметь место при реализации задания. В данном случае критерием Ф являются общие затраты системы. Любой элемент несёт определённые затраты, кот. имеют следующий вид
Имея возможность своими сообщениями влиять на те решения, которые принимает центр элементы постараются сообщить такую информацию, чтобы было принято наиболее выгодное для них решение, т.е. та информация, которую сообщает элемент не обязательно будет достоверной. Этот эффект искажения информации называется эффектом манипулирования информацией.
1. данное равновесие не всегда единственное, в этом случае вводятся дополнительные предложения, чтобы устранить неопределенность 2. равновесие по Нэшу не устойчиво к отклонению двух и более игроков. 15. Моделирование двухуровневой системы с использованием метода формирования данных. Будем считать, что наша орг.система состоит из 2 уровней: центральный орган-орган управления, решает задачу планирования деятельности n-исполнит-х (производ.)элементов, будем считать эти элементы однотипными. Планирование выражается в назначении задания каждому производственному элементу по объёму выпускаемой продукции.xi-план. задание по объёму выпускаемой продукции каждому i-му элементу.
Х1 хn
Исходим из того, что система в целом должна произвести R продукции. При этом центр стремиться минимизировать общие затраты, которые будут иметь место при реализации задания. В данном случае критерием Ф являются общие затраты системы. Любой элемент несёт определённые затраты, кот. имеют следующий вид Затраты пропорциональны квадрату количества выпускаемой продукции и обратно пропорциональны некоторому показателю ri.-показатель эффективности работы i-го предприятия. Чем больше значение этого показателя, тем меньше будут затраты.
r1 r2
x
Эффективность больше при r2. Минимизация затрат запишется следующим образом:
L=Σ хi2/2ri+ М(R-Σхi);
Это мы рассмотрели детерминированный случай, т.е. случай полной информированности центра. Но в реальных ситуациях центр не обладает в полной мере достоверной информацией об ri и руководствуется сообщаемыми заявками Si.,т.е. открывает возможность перед элементами проявить активность. Центр, приняв заявки, формирует свою целевую функцию:
Имея возможность своими сообщениями влиять на те решения, которые принимает центр элементы постараются сообщить такую информацию, чтобы было принято наиболее выгодное для них решение, т.е. та информация, которую сообщает элемент не обязательно будет достоверной. Этот эффект искажения информации называется эффектом манипулирования информацией.
3. данное равновесие не всегда единственное, в этом случае вводятся дополнительные предложения, чтобы устранить неопределенность 4. равновесие по Нэшу не устойчиво к отклонению двух и более игроков.
16. Механизм организации горизонтального согласования в задачи «поставщик-потребитель». Рассмотрим систему, состоящую из 2 предприятий. Пусть эти предприятия будут монополистами.1 предприятие производит полуфабрикат в объёме X и продаёт его по цене Ц. 2 предприятие покупает этот полуфабрикат у 1 предприятия и изготавливает из него конечный продукт в объёме Y и продаёт на рынке по рыночной цене Цр.Ставится задача об определении величины Ц, которая устраивала бы оба предприятия.
Пусть имеется некоторая взаимосвязь между количеством полуфабриката и количеством выпускаемой продукции: У = γ*х. γ- норматив затрат полуфабриката на производство готовой продукции. Обозначим через а1-норматив затрат на производство единицы полуфабриката 1 предприятием, тогда затраты 1 предприятия З1=а1*X. а2-норматив затрат на производство ед. готовой продукции вторым предприятием. Тогда затраты 2 предприятия Необходимо построить ОДР
    
У
0 а1 (Цр –а2)γ
При Ц = а1 прибыль 2-го будет максимальная, а Пр1 = 0 При Ц = (Цр –а2)γ Пр1 будет максимальная, а Пр2 = 0. (Ц-а1 )х=(Цр γ – а2γ – Ц)х; Ц= 2. Принцип равнорентабельности. В качестве показателя взаимовыгодности контактов берем рентабельность.
3. Принцип нормативного распределения рентабельности.Предположим, что имеются некоторые базовые значения рентабельностей, и договаривающиеся стороны приходят к заключению сохранить пропорции исходных рентабельностей. При этом вводится коэффициент
17.Оценка эффективности инвестиционных проектов. Под инвестициями понимается вложение финансовых средств с целью получения прибыли. Пусть имеется некоторая сумма денег
-показывает насколько эффективно работают вложенные средства. Рентабельность инвестиций как относительный показатель очень удобна при выборе одного проекта из ряда альтернативных, имеющих примерно одинаковые значения чистой текущей стоимости инвестиций, либо при комплектовании портфеля инвестиций, т.е. выборе нескольких различных вариантов одновременного инвестирования денежных средств, дающих чистую текущую стоимость.6. Внутренняя норма доходности представляет собой ту расчетную ставку процента (ставку дисконтирования), при которой сумма дисконтированных доходов за весь период использования ИП становится равной сумме первоначальных затрат (инвестициям). Иначе можно сказать, что внутренняя норма прибыли – процентная ставка, при которой чистая приведенная стоимость становится равной нулю. В заключении важно отметить, что инвестиционный проект считается привлекательным, если показатель чистого дисконтированного дохода на конец срока реализации проекта больше нуля.
|

 n хi2
n хi2 Ф = å → min
Ф = å → min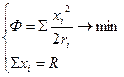 di ≤ ri ≤ Di Метод гарантированного результата заключается в том, что центр исходит из наихудшей для себя гипотезы и руководствуясь этим принимает решение. Параметры системы, по которым принимается решение разделяются на 2 класса: хорошие -рост которых способствует росту критерия определённости; плохие-рост приводит к уменьшению критерия определённости.
di ≤ ri ≤ Di Метод гарантированного результата заключается в том, что центр исходит из наихудшей для себя гипотезы и руководствуясь этим принимает решение. Параметры системы, по которым принимается решение разделяются на 2 класса: хорошие -рост которых способствует росту критерия определённости; плохие-рост приводит к уменьшению критерия определённости.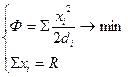 ;
; 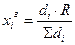 -закон планирования в условиях неопределённости, когда используется минимальная оценка. С т.зрения центра затраты равны
-закон планирования в условиях неопределённости, когда используется минимальная оценка. С т.зрения центра затраты равны  .Каждый элемент получил задание, причём работать он будет по ri, какое у него есть в реальности. Т.е. в реальности
.Каждый элемент получил задание, причём работать он будет по ri, какое у него есть в реальности. Т.е. в реальности  -данный результат не лучшая ситуация, большая упущенная выгода, недополучение возможной полезности, однако этот метод понятен и лёгок в исполнении.
-данный результат не лучшая ситуация, большая упущенная выгода, недополучение возможной полезности, однако этот метод понятен и лёгок в исполнении. r
r
 +δ
+δ имеющаяся ретроинформ. …….
имеющаяся ретроинформ. ……. .. … -δ
.. … -δ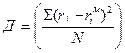 ;
; 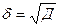 -средний квадрат отклонения расчётных экспериментальных данных.
-средний квадрат отклонения расчётных экспериментальных данных.  -истинное значение. Необходимо рассчитать з варианта: rм –модельное значение;
-истинное значение. Необходимо рассчитать з варианта: rм –модельное значение;  - пессимистическое значение;
- пессимистическое значение; 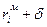 -оптимистическое значение. Данный метод применим для медленнореализуемых процессов.
-оптимистическое значение. Данный метод применим для медленнореализуемых процессов. .Затраты пропорциональны квадрату количества выпускаемой продукции и обратно пропорциональны некоторому показателю ri.-показатель эффективности работы i-го предприятия. Минимизация затрат запишется следующим образом:
.Затраты пропорциональны квадрату количества выпускаемой продукции и обратно пропорциональны некоторому показателю ri.-показатель эффективности работы i-го предприятия. Минимизация затрат запишется следующим образом: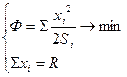 ;
;  -план,получаемый агентом зависит не только от его собственной оценки, но и от совокупных оценок др. агентов. Целевая функция элемента будет иметь следующий вид:
-план,получаемый агентом зависит не только от его собственной оценки, но и от совокупных оценок др. агентов. Целевая функция элемента будет иметь следующий вид:
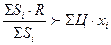 .Обозначим через V- желаемый объем производства, а через R –требуемый. Рассмотрим 3 случая: 1.V>R, Sip = Di; 2.V<R, Sip = di. 3.V=R, Sip =ri- равновесное состояние (состояние Нэша) – устойчивым исходом взаимодействия элементов можно считать такой вектор действий, от которого в одиночку никому не выгодно отклонятся. Это значит, что ни один из элементов в одиночку менять свою стратегию не может увеличить свой выигрыш при условии, что остальные элементы своих стратегий не меняют. Преимущества равновесия Нэша: 1. в большинстве моделей это равновесие существует, его можно определить. Недостатки равновесия Нэша:
.Обозначим через V- желаемый объем производства, а через R –требуемый. Рассмотрим 3 случая: 1.V>R, Sip = Di; 2.V<R, Sip = di. 3.V=R, Sip =ri- равновесное состояние (состояние Нэша) – устойчивым исходом взаимодействия элементов можно считать такой вектор действий, от которого в одиночку никому не выгодно отклонятся. Это значит, что ни один из элементов в одиночку менять свою стратегию не может увеличить свой выигрыш при условии, что остальные элементы своих стратегий не меняют. Преимущества равновесия Нэша: 1. в большинстве моделей это равновесие существует, его можно определить. Недостатки равновесия Нэша:


 z
z
 -показывает сколько единиц производственной программы приходится на ед.эффективности
-показывает сколько единиц производственной программы приходится на ед.эффективности – закон планирования, обеспечивающий мин. Затрат. di ≤ ri ≤ Di
– закон планирования, обеспечивающий мин. Затрат. di ≤ ri ≤ Di

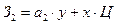 . Существует несколько подходов к определению цены:1.Принцип равных прибылей, который заключается в равенстве прибылей 1 и 2 предприятия.
. Существует несколько подходов к определению цены:1.Принцип равных прибылей, который заключается в равенстве прибылей 1 и 2 предприятия. 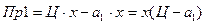 ;
; 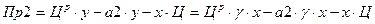 ; Пр1=Пр2
; Пр1=Пр2
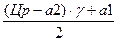

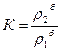 , показывающий насколько рентабельность 2-го больше или меньше рентабельности 1-го. Тогда реализация этого принципа р2 = К · р1
, показывающий насколько рентабельность 2-го больше или меньше рентабельности 1-го. Тогда реализация этого принципа р2 = К · р1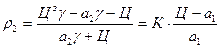 Получится следующее уравнение:
Получится следующее уравнение:
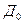 в момент времени
в момент времени  . Введём характеристику
. Введём характеристику  ,которая называется нормой дисконтирования. Значит Формула сложных процентов Дi= Д0+aД0=Д0(1+a)i. Эта формула используется для оценки фактической ст-ти капитала при пересчете из прошлого в будущее.Будущие деньги дешевеют, чем больше
,которая называется нормой дисконтирования. Значит Формула сложных процентов Дi= Д0+aД0=Д0(1+a)i. Эта формула используется для оценки фактической ст-ти капитала при пересчете из прошлого в будущее.Будущие деньги дешевеют, чем больше  Эффективность – соотношение получаемого результата с теми затратами, которые необходимо сделать.Сущ. Два типа оценки эффективности: Абсолютная оценка -результат минус затраты: Ф= Э- Z. Относительная оценка Ф= Э- Z/ Z.Оценка эффективности инвестиционного проекта: Пусть Кi – единовременные затраты; Вi – доход, который будет получен от реализации продукции Выручка в различные периоды времени имеет разную стоимость; Zi текущие затраты; Доход Дi, который будет определяться как Вi - Zi; Ток- срок жизни ИП – это время, в течение которого будет работать и приносить прибыль данный ИП.. Оценку эффективности рекомендуется проводить по системе следующих взаимосвязанных показателей: 1. КД= 1 \ (1+a)i-коэффициент дисконтирования, показывает во сколько раз уменьшится стоимость денег в I момент времени, отнесённый к начальному периоду;2. ДД – доход, приведенный к начальному моменту времени, ДДi =Дi* КД;3. ЧДД – чистый дисконтированный доход. ЧДД = Sni=1 ((Вi - Zi) - Кi) \ (1+a)i 4. Tок-срок окупаемости единовременных вложений, чем меньше срок окупаемости, тем проект привлекательнее.5.Рентабельность проекта
Эффективность – соотношение получаемого результата с теми затратами, которые необходимо сделать.Сущ. Два типа оценки эффективности: Абсолютная оценка -результат минус затраты: Ф= Э- Z. Относительная оценка Ф= Э- Z/ Z.Оценка эффективности инвестиционного проекта: Пусть Кi – единовременные затраты; Вi – доход, который будет получен от реализации продукции Выручка в различные периоды времени имеет разную стоимость; Zi текущие затраты; Доход Дi, который будет определяться как Вi - Zi; Ток- срок жизни ИП – это время, в течение которого будет работать и приносить прибыль данный ИП.. Оценку эффективности рекомендуется проводить по системе следующих взаимосвязанных показателей: 1. КД= 1 \ (1+a)i-коэффициент дисконтирования, показывает во сколько раз уменьшится стоимость денег в I момент времени, отнесённый к начальному периоду;2. ДД – доход, приведенный к начальному моменту времени, ДДi =Дi* КД;3. ЧДД – чистый дисконтированный доход. ЧДД = Sni=1 ((Вi - Zi) - Кi) \ (1+a)i 4. Tок-срок окупаемости единовременных вложений, чем меньше срок окупаемости, тем проект привлекательнее.5.Рентабельность проекта


