Задача распределения производственной программы в двухуровневой активной системе.
Организационные системы характеризуются иерархичностью. У иерархии существуют уровни подчинения. В качестве базовой модели организационной системы будем рассматривать двухуровневую модель:1) достаточно проста; 2) позволяет моделировать процессы функционирования системы; 3)результаты анализа функционирования могут служить основой для обобщения выводов по более сложным организационным системам Ф(х)
 
Fi(x,y) Yn Центр вырабатывает управляющее воздействие Х на основе критерия. Управляющее воздействие Центра направлено на оптимизацию процессов функционирования всей системы. На основе Х активные элементы начинают действовать и добиваются результатов у, т.е. у – результат деятельности.
х ÎХ
Центр вырабатывает плановые значения или задания (т.е. управленческие решения). Тогда х0 - желаемое состояние системы с точки зрения Центра. В идеале х0 =у. Введем функцию двух переменных: f (x,y) – формализованное описание целевых установок активных элементов. На этапе реализации плановых заданий активные элементы начинают трансформировать установки Х через призму своих интересов, т.е. согласно своей целевой функции. Для нормального (оптимального) функционирования организационной системы необходимо решать задачи согласования интересов целевых функций всех участников взаимодействия. Центр планирует производственные задания для n однотипных предприятий. Система в целом должна произвести R продукции. Необходимо найти плановые задания по объему производства каждого элемента системы. При этом Центр стремится минимизировать общие затраты от реализации задания. Пусть затраты активных элементов описываются следующим образом: хi2
2ri хi – объем производства каждого предприятия ri – показатель эффективности работы i-того предприятия (комплексный показатель: уровень квалификации, уровень технической оснащенности…), чем он выше, тем меньше затраты Ф- критерий, отражающий суммарные затраты
i=1 2ri n å хi = R i=1 Задача решается с пом. метода множителей Лагранжа.Получим: Центр не владеет достоверной инф-й об ri, в этом случае необходимо исп-ть методы снятия неопределенности (метод гарантированного результата, метод статистического моделирования, метод формирования данных).
|



 х1 … хn
х1 … хn

 Ф (х) → max
Ф (х) → max Zi = - функция затрат
Zi = - функция затрат n хi2
n хi2 Ф = å → min
Ф = å → min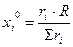 закон планирования, обеспечивающий минимум затрат. di ≤ ri ≤ Di(допустим. пределы изменения эф-ти iго элемента)
закон планирования, обеспечивающий минимум затрат. di ≤ ri ≤ Di(допустим. пределы изменения эф-ти iго элемента)


