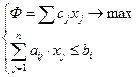Постановка задачи линейного программирования и ее экономическая трактовка

Задачи, в которых переменные и критерии в ограничениях находятся в первой степени, называются задачами линейного программирования.

Общий вид задачи:

Ф (х) ® max

x Î X

 

Любую задачу линейного программирования можно свести к стандартной форме, так наз. «основной задаче линейного программирования», которая формулируется так: найти неотрицательные значения переменных х₁, х₂, …, х_n, которые удовлетворяли бы условиям-равенствам

а₁₁ х₁+а₁₂х₂+…+а_1nх₂<=b₁

а₂₁ х₁+а₂₂х₂+…+а_2nх₂<=b₂

……………………………

а_m1 х₁+а_m2х₂+…+а_mnх₂<=b_m

и обращали бы в максимум линейную функцию этих переменных: Ф=C₁x₁+ C₂x₂+…+ C_nx_n – max/min, где Ф – критерий управления. Критерий может быть положительным (доход) и отрицательным (себестоимость), и в зависимости от знака управленческие задачи решаются на max/min. При решении подобного класса задач существует 2 подхода:

1. Прямой подход подразумевает, что существует некоторая конечная цель (техн., орг., полит.), и далее рассчитываются затраты, необходимые для достижения этой цели.

2. Обратный подход: фиксируются средства, которыми располагает лицо, принимающее решение, и далее ищутся те решения, которые наилучшим образом используют эти средства.

x_j- количество продукции j типа, b_i- запас i ресурса, c_j- цена за единицу продукции j типа, a_ij- количество ресурса i типа для производства единицы продукции j типа. Это все входные характеристики модели

x_j ⁰ – оптимальное решение, y_i – запасы ресурса i –го вида,Ф(х⁰)- ожидаемая выручка.

Это выходные характеристики данной модели (результат решения оптимизационной задачи).

Обозначим через у_i = b_i - å а_ijх _j;

_{j = 1}

у_i показывает, сколько остается в распоряжении i-того ресурса после реализации оптимальной производственной программы. Фактически это резерв по какому-либо ресурсу.

Ресурсы, для которых резервы равны 0 называются дефицитными, то есть они потребляются полностью.

Ресурсы, для которых резервы не равны 0 – недефицитные.