Проектирование систем материального стимулирования как инструмент целеполагания.
Система стимулирования – совокупность правил, по которым центр вознаграждает исполнителя за достигнутые им результаты.
Рассмотрим построение системы материального стимулирования на примере лечебного учреждения. Целевая функция исполнителя м.б. представлена следующим образом: 1. порядок формирования фондов оплаты труда (определение параметра α – норматив отчислений в фонд заработной платы); 2. порядок распределения фонда оплаты труда между исполнителями. Исследование можно начать с моделирования распределения фондов оплаты труда между исполнителями. Будем считать, что объем услуг измеряется в нормо-часах. Предположим, что T – общий объем заявок на медицинские услуги ti – объем работ, выполненный i- исполнителем. Тогда коэффициент трудового участия каждого работника Заработок i-работника в данном случае определяется
В общем случае целевая функция, определяющая поведение работников может быть записана как Проблема использования функции fi(t) заключается в корректной идентификации функций затрат ci(t). Для решения этой проблемы воспользуемся методом экспертных оценок. В качестве экспертов будут выступать работники, рассматриваемого медицинского учреждения. Вопрос ставится следующим образом: какая минимальная почасовая ставка оплаты труда вас удовлетворила бы.
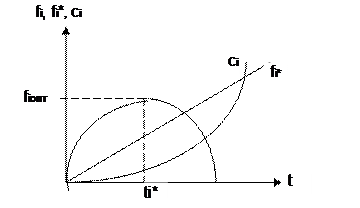
Предположим, что результаты экспертизы выглядят следующим образом (см. рисунок). Данная линейная зависимость описывается аналитической моделью Целевая функция исполнителя с учетом функции μ(t) приобретает следующий вид
Из данного графика видно, что целевая функция исполнителя увеличивается до определенного значения ti*, при этом значении достигает своего максимума, а дальше начинает убывать. Можно сделать вывод о том, что исполнитель будет выбирать для себя такую стратегию поведения (количество отработанных нормо-часов), которая будет равна ti*.
19. Моделирование уравнительной оплаты труда. Рассмотрим бригаду, состоящую из 2 рабочих. Они выпускают однотипную продукцию. П1 и П2 - их плановые задания. Каждая штука продукции дает 1 рубль в фонд оплаты труда. ФОТ = х1 + х2 – объем продукции, выпускаемой рабочими. х1, х2-количество продукции, которое сделает 1 и 2 рабочий. Тогда заработок составит f1 = f2 = (х1 + х2)/2 - уравнительная система оплаты труда. Вводим А1 и А2 – предельный объем производства продукции, который может выполнить 1 и 2 рабочий. С учётом этого строим функцию (Аi – xi) – функция комфортности труда, т.е. если x=0, то комфортность А=0. Если рабочий будет работать, то комфортность будет =0. Пусть П1 = 9 П2 = 10 А1 = 20 А2 = 22 Составим таблицу решений
Псевдооптимальная точка- в этой точке согласуются интересы центра и интересы элементов. Эта точка не является равновесной, т.к. у каждого элемента есть возможность улучшить свои возможности. Вывод: уравнительная система оплаты труда не приводит к росту производительности труда; уравнительная система оплаты труда используется при централизованной системе планирования. 20. Моделирование сдельной оплаты труда. Рассмотрим бригаду, состоящую из 2 рабочих. Они выпускают однотипную продукцию. П1 и П2 - их плановые задания. Каждая штука продукции дает 1 рубль в фонд оплаты труда. Вводим А1 и А2 – предельный объем производства продукции, который может выполнить 1 и 2 рабочий. С учётом этого строим функцию (Аi – xi) – функция комфортности труда, т.е. если x=0, то комфортность А=0. Если рабочий будет работать, то комфортность будет =0. Тогда заработок составит f1 = f2 =(Аi – xi)* xi - сдельная система оплаты труда(форма оплаты, при которой заработок зависит от количества произведённой продукции). Оптимальная стратегия в данном случае будет
Такое положение является и оптимальным и равновесным. 21. Использование таблиц решений в задачах управления. Предположим, что имеется некоторый ряд возможных управленческих решений. Всякое решение приводит к тому, что ЛПР получает некоторый фиксированный доход. Однако величина этого дохода определяется теми условиями, которые сложатся при реализации решения. В общем виде таблица решений имеет вид:
aij – доход при принятом решении j и ситуации i. После формирования таблицы решений, необходимо выработать критерии, которые позволяют конкретизировать управленческие решения. 1. Критерий Вальда (аналог гарантированного результата) Ф = max min aij j i Для каждой будущей ситуации выбирается такое управленческое решение, которое максимизирует минимальный доход. 2. Максимизация средней величины S aij
N выбирается решение j, которое обеспечивает наибольший средний выигрыш. 3. Вероятностный подход делается допущение, что ситуации не равновероятны. 0 £ рi £ 1 рi определяет вероятность того, что ситуация сложится по сценарию i. min Ф = S рi aij max i S рi = 1 4. Ф = max min aij j i
22.Многокритериальность в задачах принятия решений. Имеется некоторая система, деятельность которой определяется рядом показателей, определяющих состояние данной системы. Каждый из этих показателей отражает одно из свойств системы. Прибыль как разность выручки и затрат может характеризовать работу системы. Пусть xi-исходные параметры модели. Показатели системы имеют различный смысл, могут колебаться в различных диапазонах, иметь различную размерность. Задача нормирования исходных показателей-1.необходимо избавиться от размерности; 2.свести исходные показатели к некоторой единой базе. Вводится так называемый нормируемый показатель
|

 -модель системы стимулирования. Обозначим через c(y)-стоимостной эквивалент, который несёт исполнитель при достижении результата.
-модель системы стимулирования. Обозначим через c(y)-стоимостной эквивалент, который несёт исполнитель при достижении результата. . Для функционирования системы необходимо, чтобы
. Для функционирования системы необходимо, чтобы  . Целевая функция центра м.б. представлена следующим образом:
. Целевая функция центра м.б. представлена следующим образом:  .Рассмотрим проектирование систем материального стимулирования на примере медицинского учреждения. Создание материального стимула в виде фондов оплаты труда предполагает формирование заинтересованных исполнителей в высокоэффективном труде. Имеются два фактора, определяющих поведение исполнителей:
.Рассмотрим проектирование систем материального стимулирования на примере медицинского учреждения. Создание материального стимула в виде фондов оплаты труда предполагает формирование заинтересованных исполнителей в высокоэффективном труде. Имеются два фактора, определяющих поведение исполнителей:

 , где α – норматив отчислений в фонд заработной платы.
, где α – норматив отчислений в фонд заработной платы. , где ci – стоимостной эквивалент затрат работника на выполнение некоторого объема работы.
, где ci – стоимостной эквивалент затрат работника на выполнение некоторого объема работы.
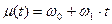 , где ω – функция затрат исполнителя.
, где ω – функция затрат исполнителя.
 – функция удовлетворенности трудом.
– функция удовлетворенности трудом. 104,5
104,5
 115,5
115,5
 :
:

 Ф = max
Ф = max ,
,  -некоторая точка отсчёта(например, плановое задание конкретного исполнителя), значение данного показателя может определять предшествующий период или нормативы. Возникает задача многокритериальных оценок.
-некоторая точка отсчёта(например, плановое задание конкретного исполнителя), значение данного показателя может определять предшествующий период или нормативы. Возникает задача многокритериальных оценок. - суммируются
- суммируются  ,исходя из того, что
,исходя из того, что 


