Упражнения к § 1
1. Доказать, что множество всех функций со значениями в данном поле K, определенные на множестве из n элементов, составляют n-мерное векторное пространство над полем K по отношению к действиям сложения функций и умножения на константу поля K.
2. В множестве 1) «сложения» 2) «умножения на действительное число» Проверить, что множество
3. Будет ли множество всех многочленов 1) f(0)=1; f(1)=0; 2) 2f(0)-3f(1)=0.
4. Пусть 1. 2. Будет ли
5. Доказать, что система векторов, содержащая нулевой вектор, линейно зависима.
6. Выяснить, являются ли следующие системы векторов арифметических пространств линейно зависимыми: 2. 3. 4.
7. Найти все значения параметра 1. 2.
8. Являются ли многочлены
9. Векторы 1) 2)
3) 4)
10. Систему векторов
11. Показать, что следующие системы векторов являются базисами пространства 1)
2)
12. Проверить, какая из следующих систем векторов является базисом пространства 1)
2)
13. Найти координаты многочлена 1) 1, t+ 1, 2)
§ 2. Линейные подпространства. Прямая сумма подпространств. Произведение пространств
Определение 1. Подмножество M из линейного пространства X над полем K называется линейным подпространством, если: 1) 1) для любых Каждое подпространство является самостоятельным линейным пространством. Задача 1. Доказать, что линейная оболочка, натянутая на систему векторов Решение. Проверим свойства линейного подпространства. Рассмотрим элементы Так как Тогда Аналогично Таким образом, доказано, что данное множество является линейным подпространством.
Задача 2. Докажите, что n-мерные векторы пространства Решение. Пусть Докажем, что M – подпространство: Рассмотрим векторы 2. Рассмотрим Тогда Таким образом, что M – подпространство. Найдем базис и размерность в подпространстве M. Рассмотрим векторы подпространства M:
|

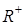 положительных действительных чисел определены операции:
положительных действительных чисел определены операции: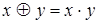 ;
;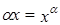 .
.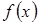 , удовлетворяющих следующим условиям, линейным пространством относительно обычных операций сложения и умножения на число:
, удовлетворяющих следующим условиям, линейным пространством относительно обычных операций сложения и умножения на число: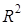 – множество всех упорядоченных пар действительных чисел
– множество всех упорядоченных пар действительных чисел 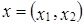 с операциями:
с операциями: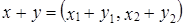 ;
;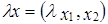 .
. (-3, 1, 5);
(-3, 1, 5); 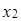 = (6, -2, 15);
= (6, -2, 15);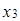 =(3, 7, 11);
=(3, 7, 11);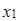 =(2, -3, 1);
=(2, -3, 1);  , при которых вектор b линейно выражается через векторы
, при которых вектор b линейно выражается через векторы 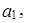
 ,
, 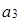 :
: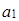 =(3, 4, 2);
=(3, 4, 2);  b =(9, 12, l);
b =(9, 12, l); линейно независимыми:
линейно независимыми:  ,
, 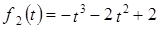 ,
, 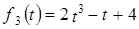 ?
? и x заданы своими координатами в некотором базисе. Показать, что
и x заданы своими координатами в некотором базисе. Показать, что  =(2, 1, -3),
=(2, 1, -3),  =(3, 2, -5),
=(3, 2, -5),  =(1, -1, 1), x =(6, 2, -7);
=(1, -1, 1), x =(6, 2, -7); =(1, 3, -1, 0); x= (7, 14, -1, 2);
=(1, 3, -1, 0); x= (7, 14, -1, 2); .
.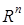 :
: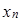 =(0, 0, 0, …, n);
=(0, 0, 0, …, n); :
: =(1, 3, -1, 0);
=(1, 3, -1, 0);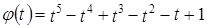 в каждом из следующих базисов пространства
в каждом из следующих базисов пространства  :
: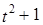 ,
,  ,
, 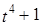 ,
,  ;
;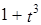 ,
, 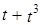 ,
,  ,
, 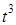 ,
,  ,
, 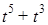 .
.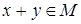 ;
;
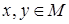 ,
,  .
. из пространства X:
из пространства X: 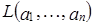 , является линейным подпространством пространства X.
, является линейным подпространством пространства X.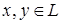 и
и  ,
, 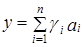 , где
, где 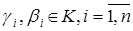 .
. , где
, где 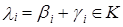 . Таким образом,
. Таким образом, 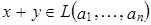 .
.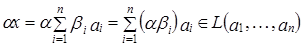 .
.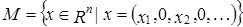 .
.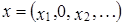 ,
, 
 . Тогда
. Тогда  , где
, где  .
. .
.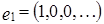 ,
, 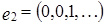 ,
, 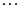 , где вектор
, где вектор  имеет 1 на (2k-1) - ом месте, а остальные координаты равны 0.
имеет 1 на (2k-1) - ом месте, а остальные координаты равны 0.


