Рассмотрим 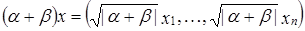 ,
, 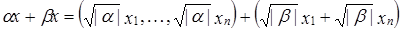 =
=  .
.
Так как 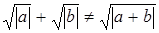 ,
, 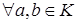 , то свойство 7) линейных пространств в данном примере не выполнено.
, то свойство 7) линейных пространств в данном примере не выполнено.
Примерами линейных пространств являются:
1. Множество  всех функций действительного переменного, определенных и непрерывных на отрезке
всех функций действительного переменного, определенных и непрерывных на отрезке 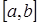 , с обычными правилами сложения функций и умножения их на действительные числа.
, с обычными правилами сложения функций и умножения их на действительные числа.
2. Множество 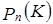 многочленов степени не выше n с коэффициентами из поля K с обычными операциями сложения многочленов и умножения на числа поля K.
многочленов степени не выше n с коэффициентами из поля K с обычными операциями сложения многочленов и умножения на числа поля K.
3. Множество 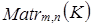 прямоугольных матриц размерности
прямоугольных матриц размерности 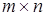 с элементами из поля K с обычными операциями сложения матриц и умножения их на числа поля K.
с элементами из поля K с обычными операциями сложения матриц и умножения их на числа поля K.
4. Множество всех векторов-решений линейной однородной системы уравнений с коэффициентами поля K относительно сложения векторов-решений и умножения их на числа поля K.
1) Линейная зависимость векторов
Пусть X – линейное пространство над полем K.
Определение 2. Вектор b из линейного пространства X называется линейной комбинацией векторов  из X, если существуют такие числа
из X, если существуют такие числа  из поля K, что
из поля K, что
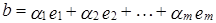 . (1)
. (1)
При этом также говорят, что вектор b линейно выражается через векторы  .
.
Определение 3. Линейной оболочкой, натянутой на некоторое множество векторов  пространства X, называется множество всевозможных линейных комбинаций векторов из P:
пространства X, называется множество всевозможных линейных комбинаций векторов из P: 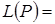
 =
=  .
.
Линейная оболочка образует линейное пространство.
Чтобы найти линейное выражение вектора 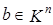 через векторы
через векторы  из
из 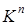 , следует записать векторное равенство (1) и от него перейти к покоординатным равенствам в силу того, что два вектора равны тогда и только тогда, когда равны их соответствующие координаты. В результате получится система n линейных уравнений относительно
, следует записать векторное равенство (1) и от него перейти к покоординатным равенствам в силу того, что два вектора равны тогда и только тогда, когда равны их соответствующие координаты. В результате получится система n линейных уравнений относительно  . Решив систему и подставив решение в равенство (1), найдем линейное выражение вектора b через
. Решив систему и подставив решение в равенство (1), найдем линейное выражение вектора b через  .
.
Поясним описанное правило на примере.
Задача 3. Найти линейное выражение вектора  через векторы
через векторы 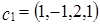 и
и  .
.
Решение.
Составим векторное равенство (1):
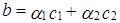 , то есть
, то есть

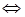
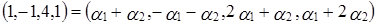 .
.
Два вектора пространства 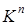 равны тогда и только тогда, когда равны их соответствующие координаты. Перейдя к покоординатным равенствам, получим систему линейных уравнений:
равны тогда и только тогда, когда равны их соответствующие координаты. Перейдя к покоординатным равенствам, получим систему линейных уравнений:

Решением системы являются числа  ,
, 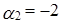 . Поэтому
. Поэтому 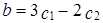 .
.
Задача 4. Найти все значение параметра  , при которых вектор
, при которых вектор  линейно выражается через векторы
линейно выражается через векторы 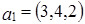 и
и 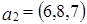 .
.
Решение.
Запишем равенство (1) для данного примера:
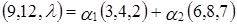 .
.
Переходя к покоординатным равенствам, получим систему:

Решение системы: 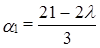 ,
,  существует и единственно при любых
существует и единственно при любых  . Следовательно, при любом действительном
. Следовательно, при любом действительном  вектор b линейно выражается через заданную систему векторов.
вектор b линейно выражается через заданную систему векторов.
Определение 4. Система векторов  из линейного пространства X называется линейно зависимой, если хотя бы один из них является линейной комбинацией остальных векторов системы.
из линейного пространства X называется линейно зависимой, если хотя бы один из них является линейной комбинацией остальных векторов системы.
Данное определение эквивалентно следующему: система векторов  из линейного пространства X называется линейно зависимой, если существуют числа
из линейного пространства X называется линейно зависимой, если существуют числа  , не равные нулю одновременно, такие, что имеет место равенство:
, не равные нулю одновременно, такие, что имеет место равенство:
 . (2)
. (2)
Векторы  , не являющиеся линейно зависимыми, называются линейно независимыми, т.е. система векторов линейно независима, если равенство (2) возможно лишь в случае
, не являющиеся линейно зависимыми, называются линейно независимыми, т.е. система векторов линейно независима, если равенство (2) возможно лишь в случае  .
.
Для того чтобы выяснить вопрос о линейной зависимости векторов  пространства
пространства 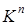 , следует рассмотреть равенство (2) и перейти от него к покоординатным равенствам. В результате получится система n линейных однородных уравнений относительно
, следует рассмотреть равенство (2) и перейти от него к покоординатным равенствам. В результате получится система n линейных однородных уравнений относительно  . Если полученная система имеет только лишь нулевое решение:
. Если полученная система имеет только лишь нулевое решение:  , то система векторов
, то система векторов  линейно независима. В противном случае (т.е. если система имеет и ненулевые решения) система векторов
линейно независима. В противном случае (т.е. если система имеет и ненулевые решения) система векторов  линейно зависима.
линейно зависима.
Задача 5. Выяснить вопрос о линейной зависимости векторов 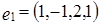 ,
,  ,
, 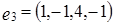 .
.
Решение.
Составим векторное равенство:
 .
.
Переходя к покоординатным равенствам, получаем систему:
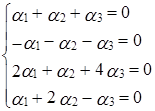
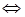
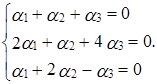
Решая систему методом Гаусса, находим, что она имеет ненулевое решение:  ,
, 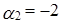 ,
, 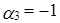 . Поэтому приведенная система векторов является линейно зависимой, причем
. Поэтому приведенная система векторов является линейно зависимой, причем 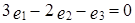 .
.
Отметим, что однородная система n уравнений с n переменными: 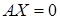 имеет ненулевое решение, если определитель матрицы A равен нулю, т.е. detA=|A|=0. В противном случае, система имеет только тривиальное (нулевое) решение. Таким образом, вопрос о линейной зависимости векторов
имеет ненулевое решение, если определитель матрицы A равен нулю, т.е. detA=|A|=0. В противном случае, система имеет только тривиальное (нулевое) решение. Таким образом, вопрос о линейной зависимости векторов  в пространстве
в пространстве 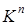 сводится к вычислению определителя матрицы системы. В задаче 5: det A =0. Следовательно, исходная система векторов линейно зависима.
сводится к вычислению определителя матрицы системы. В задаче 5: det A =0. Следовательно, исходная система векторов линейно зависима.
Задача 6. Докажите, что в пространстве  многочлены разной степени линейно независимы.
многочлены разной степени линейно независимы.
Решение.
Рассмотрим ненулевые многочлены разной степени из пространства  :
: 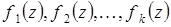 . Докажем, что из равенства
. Докажем, что из равенства 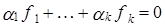 следует, что
следует, что  .
.
Предположим противное: существует  .
.
Тогда  . (3)
. (3)
Так как степени всех многочленов по условию различны, то степень многочлена 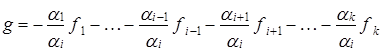 , стоящего в правой части равенства (3), равна максимальной из степеней многочленов
, стоящего в правой части равенства (3), равна максимальной из степеней многочленов  , для которых
, для которых  (такой j существует, так как
(такой j существует, так как  ), и не совпадает со степенью многочлена
), и не совпадает со степенью многочлена 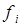 , находящегося в левой части равенства, то есть равенство (3) невозможно. Таким образом, получили противоречие, доказав линейную независимость многочленов разной степени.
, находящегося в левой части равенства, то есть равенство (3) невозможно. Таким образом, получили противоречие, доказав линейную независимость многочленов разной степени.
Задача 7. Проверить линейную независимость матриц
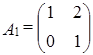 ,
, 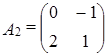 ,
,  ,
, 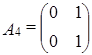
в пространстве 

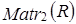 .
.
Решение.
Составим линейную комбинацию матриц:  , то есть:
, то есть:
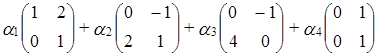 =
= 
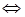
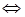
 .
.
Переходя к покоординатным равенствам, получаем систему:
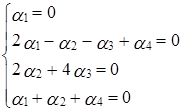
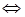
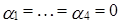 , т.е. исходная система матриц линейно независима.
, т.е. исходная система матриц линейно независима.

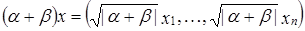 ,
, 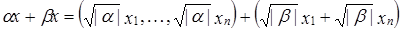 =
=  .
.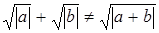 ,
, 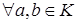 , то свойство 7) линейных пространств в данном примере не выполнено.
, то свойство 7) линейных пространств в данном примере не выполнено. всех функций действительного переменного, определенных и непрерывных на отрезке
всех функций действительного переменного, определенных и непрерывных на отрезке 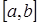 , с обычными правилами сложения функций и умножения их на действительные числа.
, с обычными правилами сложения функций и умножения их на действительные числа.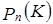 многочленов степени не выше n с коэффициентами из поля K с обычными операциями сложения многочленов и умножения на числа поля K.
многочленов степени не выше n с коэффициентами из поля K с обычными операциями сложения многочленов и умножения на числа поля K.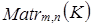 прямоугольных матриц размерности
прямоугольных матриц размерности 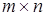 с элементами из поля K с обычными операциями сложения матриц и умножения их на числа поля K.
с элементами из поля K с обычными операциями сложения матриц и умножения их на числа поля K. из X, если существуют такие числа
из X, если существуют такие числа  из поля K, что
из поля K, что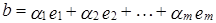 . (1)
. (1) пространства X, называется множество всевозможных линейных комбинаций векторов из P:
пространства X, называется множество всевозможных линейных комбинаций векторов из P: 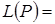
 =
=  .
.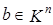 через векторы
через векторы  из
из 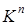 , следует записать векторное равенство (1) и от него перейти к покоординатным равенствам в силу того, что два вектора равны тогда и только тогда, когда равны их соответствующие координаты. В результате получится система n линейных уравнений относительно
, следует записать векторное равенство (1) и от него перейти к покоординатным равенствам в силу того, что два вектора равны тогда и только тогда, когда равны их соответствующие координаты. В результате получится система n линейных уравнений относительно  . Решив систему и подставив решение в равенство (1), найдем линейное выражение вектора b через
. Решив систему и подставив решение в равенство (1), найдем линейное выражение вектора b через  через векторы
через векторы 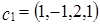 и
и  .
.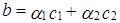 , то есть
, то есть
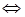
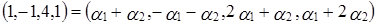 .
.
 ,
, 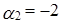 . Поэтому
. Поэтому 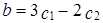 .
. , при которых вектор
, при которых вектор  линейно выражается через векторы
линейно выражается через векторы 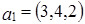 и
и 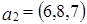 .
.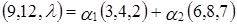 .
.
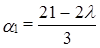 ,
,  существует и единственно при любых
существует и единственно при любых  . Следовательно, при любом действительном
. Следовательно, при любом действительном  , не равные нулю одновременно, такие, что имеет место равенство:
, не равные нулю одновременно, такие, что имеет место равенство: . (2)
. (2) .
.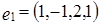 ,
,  ,
, 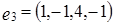 .
. .
.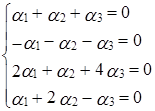
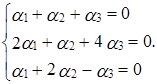
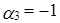 . Поэтому приведенная система векторов является линейно зависимой, причем
. Поэтому приведенная система векторов является линейно зависимой, причем 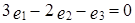 .
.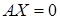 имеет ненулевое решение, если определитель матрицы A равен нулю, т.е. detA=|A|=0. В противном случае, система имеет только тривиальное (нулевое) решение. Таким образом, вопрос о линейной зависимости векторов
имеет ненулевое решение, если определитель матрицы A равен нулю, т.е. detA=|A|=0. В противном случае, система имеет только тривиальное (нулевое) решение. Таким образом, вопрос о линейной зависимости векторов  в пространстве
в пространстве  многочлены разной степени линейно независимы.
многочлены разной степени линейно независимы.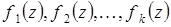 . Докажем, что из равенства
. Докажем, что из равенства 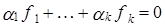 следует, что
следует, что  .
. .
. . (3)
. (3)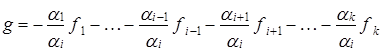 , стоящего в правой части равенства (3), равна максимальной из степеней многочленов
, стоящего в правой части равенства (3), равна максимальной из степеней многочленов  , для которых
, для которых  (такой j существует, так как
(такой j существует, так как  ), и не совпадает со степенью многочлена
), и не совпадает со степенью многочлена 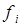 , находящегося в левой части равенства, то есть равенство (3) невозможно. Таким образом, получили противоречие, доказав линейную независимость многочленов разной степени.
, находящегося в левой части равенства, то есть равенство (3) невозможно. Таким образом, получили противоречие, доказав линейную независимость многочленов разной степени.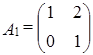 ,
, 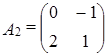 ,
,  ,
, 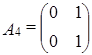

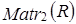 .
. , то есть:
, то есть: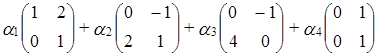 =
= 
 .
.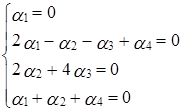
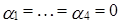 , т.е. исходная система матриц линейно независима.
, т.е. исходная система матриц линейно независима.


