Упражнения к § 5
Пусть
Вычислить скалярное произведение векторов Применить процесс ортогонализации к следующим векторам пространства
Дополнить следующую систему векторов до ортонормированных базисов: 1)
Применяя процесс ортогонализации, построить ортонормированный базис подпространства, натянутого на данную систему векторов: (1, 2, 2, -1); (1, 1, -5, 3); (3, 2, 8, -7).
Найти ортогональную проекцию вектора
Найти расстояние от точки, заданной вектором
ЛИТЕРАТУРА Воеводин В.В. Линейная алгебра. – М.: Наука, 1980. Гельфанд И.М. Лекции по линейной алгебре. – М.: Наука, 1971. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974. Баскаков А.Г. Лекции по алгебре. – Воронеж: Воронеж. ун-т, 1999. Фаддеев Д.К., Соминский Н.С. Сборник задач по высшей алгебре. – М.: Наука, 1977. Проскуряков И.В. Сборник задач по линейной алгебре. – 7-е изд. – М.: Наука, 1984. Икрамов Х.Д. Задачник по линейной алгебре. – М.: Наука, 1975. Шевцов Г.С. Линейная алгебра: Учеб.пособие. - М.: Наука, 1999.
Составители: Бондаренко Юлия Валентиновна, Глушакова Татьяна Николаевна, Тихомирова Екатерина Сергеевна
Рецензент Покорная И.Ю.
Редактор Тихомирова О.А.
|

 ,
,  – произвольные векторы пространства
– произвольные векторы пространства  . Показать, что скалярное произведение в
. Показать, что скалярное произведение в 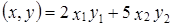 ;
;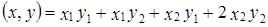 .
. и
и 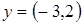 и угол между ними каждым из этих способов.
и угол между ними каждым из этих способов.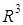 :
: 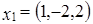 ;
;  ;
;  .
. ;
; 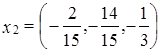 ;
;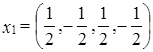 ;
;  .
. на подпространство L:
на подпространство L: , L натянуто на векторы
, L натянуто на векторы  ,
, 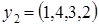 ,
, 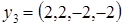 ;
;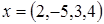 , L натянуто на векторы
, L натянуто на векторы  ,
,  ,
, 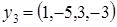 .
. , до линейного многообразия, заданного системой уравнений:
, до линейного многообразия, заданного системой уравнений: ,
,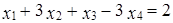 .
.


