Определение 5. Всякую систему  векторов линейного пространства X называют базисом, или базой, этого пространства, если:
векторов линейного пространства X называют базисом, или базой, этого пространства, если:
1. система векторов  линейно независима;
линейно независима;
2. любой вектор x пространства X линейно выражается через векторы этой системы:
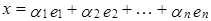 . (4)
. (4)
Числа 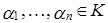 называются координатами вектора x относительно базиса
называются координатами вектора x относительно базиса  . Число n базисных векторов в пространстве X называется размерностью пространства и обозначается символом dim X.
. Число n базисных векторов в пространстве X называется размерностью пространства и обозначается символом dim X.
Задача 8. Доказать, что векторы вида:  ,
,  ,
, 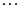 ,
, 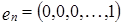 образуют базис в пространстве
образуют базис в пространстве 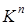 .
.
Решение.
Докажем линейную независимость векторов  .
.
Рассмотрим линейную комбинацию:



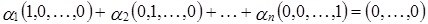


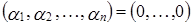


 ,
,
т.е.  линейно независимы.
линейно независимы.
Покажем, что для любого вектора  справедливо представление (4).
справедливо представление (4).
Пусть  . Тогда
. Тогда  , т.е. коэффициенты
, т.е. коэффициенты  равенства (4) в данном примере совпадают с
равенства (4) в данном примере совпадают с  .
.
Таким образом, исходная система векторов является базисом в пространстве 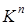 и dim
и dim 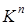 =n.
=n.
Аналогично можно доказать следующие утверждения:
1. Многочлены 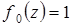 ,
, 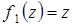 ,
, 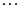 ,
, 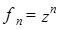 образуют базис в линейном пространстве
образуют базис в линейном пространстве 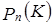 , где K =R или K =C;
, где K =R или K =C; 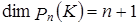 .
.
2. В линейном пространстве 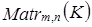 матриц размерности
матриц размерности 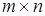 базисом являются матрицы
базисом являются матрицы  ,
,  ,
,  , где
, где  – матрица, на пересечении i-ой строки которой и j-го столбца стоит единица, а остальные элементы – нули.
– матрица, на пересечении i-ой строки которой и j-го столбца стоит единица, а остальные элементы – нули.

 векторов линейного пространства X называют базисом, или базой, этого пространства, если:
векторов линейного пространства X называют базисом, или базой, этого пространства, если: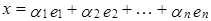 . (4)
. (4)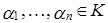 называются координатами вектора x относительно базиса
называются координатами вектора x относительно базиса  ,
,  ,
, 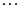 ,
, 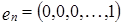 образуют базис в пространстве
образуют базис в пространстве 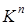 .
.

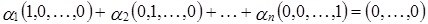
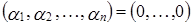
 ,
, справедливо представление (4).
справедливо представление (4). . Тогда
. Тогда  , т.е. коэффициенты
, т.е. коэффициенты  равенства (4) в данном примере совпадают с
равенства (4) в данном примере совпадают с  .
.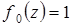 ,
, 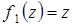 ,
, 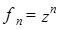 образуют базис в линейном пространстве
образуют базис в линейном пространстве 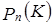 , где K =R или K =C;
, где K =R или K =C; 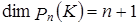 .
.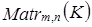 матриц размерности
матриц размерности 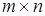 базисом являются матрицы
базисом являются матрицы  ,
,  ,
,  , где
, где 


