Докажем, что 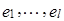 образуют базис.
образуют базис.
1. Проверим линейную независимость 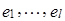 .
.
Составим линейную комбинацию:


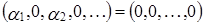

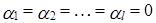 .
.
2. Для любого 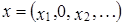
 справедливо:
справедливо:  .
.
Таким образом, доказано, что 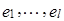 – базис в линейном подпространстве M и
– базис в линейном подпространстве M и  .
.
Задача 3. Доказать, что все n-мерные векторы вида 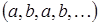 , где
, где  a, b – любые числа поля K образуют линейное подпространство M. Найти его размерность и базис.
a, b – любые числа поля K образуют линейное подпространство M. Найти его размерность и базис.
Решение.
1. Докажем, что множество  является линейным подпространством.
является линейным подпространством.
Рассмотрим векторы 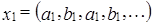 ,
, 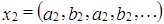 . Тогда
. Тогда  , где
, где 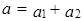 ,
, 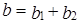 .
.
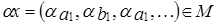 .
.
Таким образом, M – линейное подпространство.
1. Найдем базис и размерность M.
Рассмотрим векторы 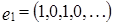 ,
,  . Векторы
. Векторы 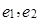 линейно независимы (доказать самостоятельно) и для любого вектора пространства M справедливо:
линейно независимы (доказать самостоятельно) и для любого вектора пространства M справедливо: 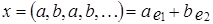 . Таким образом,
. Таким образом, 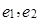 – базис в подпространстве M и dim M =2.
– базис в подпространстве M и dim M =2.
Задача 4. Проверить, является ли подмножество M пространства 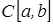 непрерывных на отрезке
непрерывных на отрезке 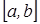 функций линейным подпространством, если
функций линейным подпространством, если  .
.
Решение.
Рассмотрим 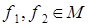 . Тогда
. Тогда 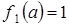 ,
,  . Так как сумма двух непрерывных функций является непрерывной функцией, то нам остается проверить выполнение равенства:
. Так как сумма двух непрерывных функций является непрерывной функцией, то нам остается проверить выполнение равенства:
 .
.
Рассмотрим 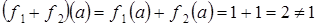 . Таким образом, M не является линейным пространством.
. Таким образом, M не является линейным пространством.
Задача 5. Найти размерность подпространства 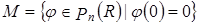 .
.
Решение.
Рассмотрим многочлен  :
: 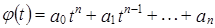 . Пусть
. Пусть 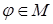 , тогда
, тогда 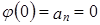 , то есть
, то есть  . Рассмотрим многочлены:
. Рассмотрим многочлены: 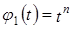 ,
, 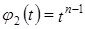 ,
, 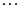 ,
, 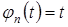 . Данная система многочленов линейно независима, так как включает многочлены разной степени и для любого многочлена подпространства M справедливо:
. Данная система многочленов линейно независима, так как включает многочлены разной степени и для любого многочлена подпространства M справедливо: 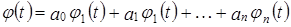 . Таким образом,
. Таким образом, 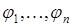 образует базис в M и dim M = n.
образует базис в M и dim M = n.
Задача 6. Найдите размерность подпространства
 .
.
Решение.
Рассмотрим многочлен  :
: 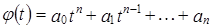 . Пусть
. Пусть 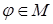 , тогда
, тогда 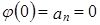 ,
, 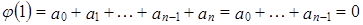 . Тогда
. Тогда 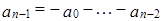 и многочлен имеет вид:
и многочлен имеет вид: 
 .
.
Рассмотрим следующие многочлены:
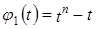 ,
,  ,
, 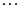 ,
, 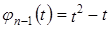 .
.
Данная система многочленов линейно независима, так как включает многочлены разной степени, и для любого многочлена пространства M справедливо: 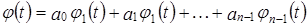 . Таким образом,
. Таким образом, 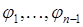 образует базис в M и dim M = n-1.
образует базис в M и dim M = n-1.
Задача 7. Рассмотрите подпространство
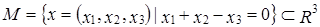
и докажите, что его размерность равна 2.
Решение.
Рассмотрим вектор  . Тогда
. Тогда 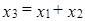 и
и  имеет вид:
имеет вид: 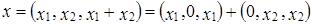 .
.
Рассмотрим векторы 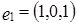 ,
, 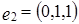 . Легко проверить, что векторы
. Легко проверить, что векторы 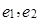 – линейно независимы и для любого
– линейно независимы и для любого 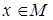 справедливо:
справедливо: 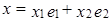 . Таким образом,
. Таким образом, 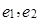 – базис подпространства M и dim M = 2.
– базис подпространства M и dim M = 2.
Задача 9. Докажите, что кососимметрические матрицы образуют линейное подпространство M пространства всех квадратных матриц порядка n над полем R. Найти базис и размерность этого подпространства.
Решение.
Матрица  называется кососимметрической, если
называется кососимметрической, если 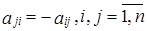 .
.
Непосредственно из определения следует, что  , т.е. матрица
, т.е. матрица  имеет вид:
имеет вид: 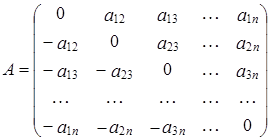 .
.
1) Докажем, что M – линейное подпространство. Рассмотрим кососимметрические матрицы 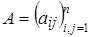 ,
, 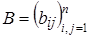 . Согласно определению,
. Согласно определению, 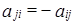 ,
, 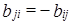 ,
, 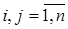 .
.
Рассмотрим матрицу  . Элементы
. Элементы 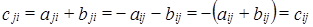 . Следовательно,
. Следовательно, 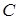 - кососимметрическая матрица.
- кососимметрическая матрица.
Рассмотрим матрицу 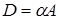 , где
, где 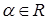 и
и 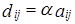 .Элементы
.Элементы  , т.е.
, т.е. 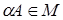 , и следовательно, M – линейное подпространство. Рассмотрим матрицы подпространства M:
, и следовательно, M – линейное подпространство. Рассмотрим матрицы подпространства M: 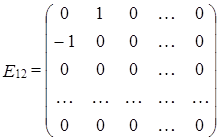 ,
, 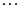 ,
, 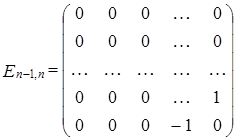 , где
, где 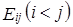 - матрица, у которой элемент
- матрица, у которой элемент  равен 1, элемент
равен 1, элемент 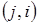 равен –1, а остальные элементы – нули. Число таких матриц
равен –1, а остальные элементы – нули. Число таких матриц 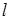 равно числу наддиагональных элементов матрицы размерности
равно числу наддиагональных элементов матрицы размерности  :
: 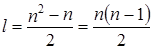 .
.
Очевидно, что матрицы  линейно независимы и любая кососимметрическая матрица представима в виде их линейной комбинации:
линейно независимы и любая кососимметрическая матрица представима в виде их линейной комбинации:
 .
.
Следовательно,  образуют базис в подпространстве M и
образуют базис в подпространстве M и
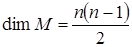 .
.
Определение 2. Линейное пространство X является прямой суммой своих подпространств  и
и  , если каждый вектор
, если каждый вектор 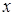 из X единственным образом можно представить в виде:
из X единственным образом можно представить в виде: 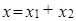 , где
, где  . Используется обозначение
. Используется обозначение  .
.
Задача 10. Докажите, что 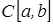 есть прямая сумма подпространства
есть прямая сумма подпространства 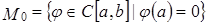 и подпространства постоянных функций
и подпространства постоянных функций  .
.
Решение.
Рассмотрим функцию 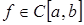 . Тогда справедливо представление:
. Тогда справедливо представление: 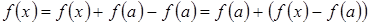 , где
, где  – константа, а функция
– константа, а функция 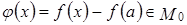 . Следовательно, любой элемент
. Следовательно, любой элемент 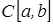 можно представить в виде суммы элементов подпространств
можно представить в виде суммы элементов подпространств 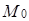 и
и 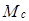 . Докажем, что такое представление единственно.
. Докажем, что такое представление единственно.
Пусть 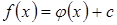 , где
, где 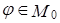 ,
, 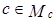 .
.
Предположим противное: существуют  ,
, 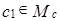 (
(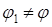 или (и)
или (и) 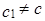 ) такие, что
) такие, что 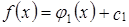 . Тогда
. Тогда 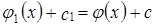 ,
, 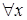 . Рассмотрим
. Рассмотрим  . Так как
. Так как 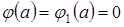 , то
, то 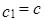 . Таким образом,
. Таким образом, 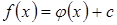 ,
, 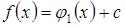 . Тогда
. Тогда 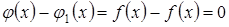 ,
, 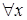 и, следовательно,
и, следовательно, 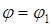 , что противоречит предположению.
, что противоречит предположению.
Таким образом,  .
.
Задача 11. Доказать, что пространство всех квадратных матриц порядка 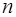 есть прямая сумма линейных подпространств
есть прямая сумма линейных подпространств 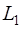 – симметрических матриц и
– симметрических матриц и 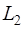 – кососимметрических матриц.
– кососимметрических матриц.
Решение.
Пусть 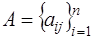 – произвольная квадратная матрица. Покажем, что ее можно единственным образом представить в виде
– произвольная квадратная матрица. Покажем, что ее можно единственным образом представить в виде 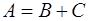 , где
, где 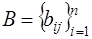 и
и 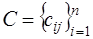 – симметрическая и кососимметрическая матрицы соответственно.
– симметрическая и кососимметрическая матрицы соответственно.
Так как 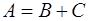 , то
, то  , откуда
, откуда 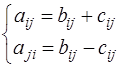 . Сложим первое и второе уравнения системы, получим
. Сложим первое и второе уравнения системы, получим 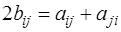 , откуда
, откуда 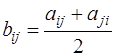 . Очевидно, что
. Очевидно, что 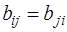 , то есть матрица
, то есть матрица  – симметрическая.
– симметрическая.
Вычтем теперь из первого уравнения системы второе. Получим  , откуда
, откуда 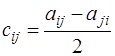 . Очевидно, что
. Очевидно, что 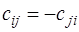 , то есть матрица
, то есть матрица 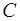 – кососимметрическая.
– кососимметрическая.
Таким образом, произвольную квадратную матрицу 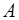 разложили на сумму симметрической и кососимметрической матриц, элементы которых определяются единственным образом, то есть пространство всех квадратных матриц порядка
разложили на сумму симметрической и кососимметрической матриц, элементы которых определяются единственным образом, то есть пространство всех квадратных матриц порядка 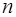 есть прямая сумма линейных подпространств
есть прямая сумма линейных подпространств 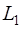 – симметрических матриц и
– симметрических матриц и 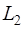 – кососимметрических матриц.
– кососимметрических матриц.
Определение 3. Пусть 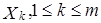 – совокупность линейных пространств, рассматриваемых над одним и тем же полем K. Их произведение
– совокупность линейных пространств, рассматриваемых над одним и тем же полем K. Их произведение 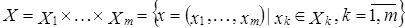 является линейным пространством, если для любой пары элементов
является линейным пространством, если для любой пары элементов 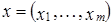 ,
, 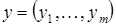 из X и числа
из X и числа  положить:
положить: 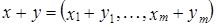 ,
, 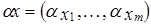 .
.
Задача 12. Найдите размерность произведения 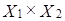 линейных пространств
линейных пространств  ,
, 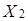 .
.
Решение.
Рассмотрим линейное пространство 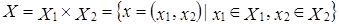 .
.
Пусть 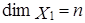 и
и  – базис в
– базис в  ;
;  и
и  – базис в
– базис в 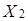 . Рассмотрим векторы пространства X вида:
. Рассмотрим векторы пространства X вида: 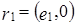 ,
, 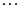
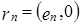 ,
, 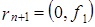 ,
, 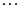 ,
,  . Докажем, что
. Докажем, что 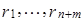 образуют базис в X.
образуют базис в X.
Проверим линейную независимость системы векторов:
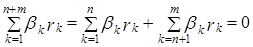



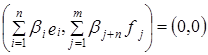

 , что в силу линейной независимости векторов
, что в силу линейной независимости векторов  и
и  эквивалентно тому, что
эквивалентно тому, что  . Таким образом, система векторов
. Таким образом, система векторов 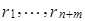 линейно независима.
линейно независима.
Рассмотрим вектор  ,
,  :
: 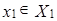 ,
, 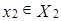 . Тогда
. Тогда 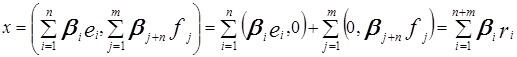 . Следовательно,
. Следовательно, 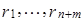 – базис в X и
– базис в X и 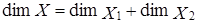 .
.

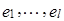 образуют базис.
образуют базис.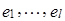 .
.

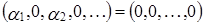
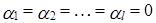 .
.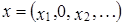
 справедливо:
справедливо:  .
. .
.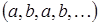 , где
, где  a, b – любые числа поля K образуют линейное подпространство M. Найти его размерность и базис.
a, b – любые числа поля K образуют линейное подпространство M. Найти его размерность и базис. является линейным подпространством.
является линейным подпространством.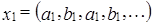 ,
, 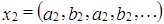 . Тогда
. Тогда  , где
, где 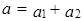 ,
, 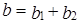 .
.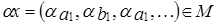 .
.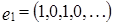 ,
,  . Векторы
. Векторы 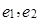 линейно независимы (доказать самостоятельно) и для любого вектора пространства M справедливо:
линейно независимы (доказать самостоятельно) и для любого вектора пространства M справедливо: 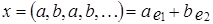 . Таким образом,
. Таким образом, 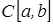 непрерывных на отрезке
непрерывных на отрезке 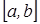 функций линейным подпространством, если
функций линейным подпространством, если  .
.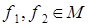 . Тогда
. Тогда 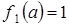 ,
,  . Так как сумма двух непрерывных функций является непрерывной функцией, то нам остается проверить выполнение равенства:
. Так как сумма двух непрерывных функций является непрерывной функцией, то нам остается проверить выполнение равенства: .
.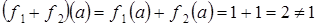 . Таким образом, M не является линейным пространством.
. Таким образом, M не является линейным пространством.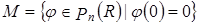 .
. :
: 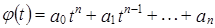 . Пусть
. Пусть 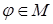 , тогда
, тогда 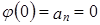 , то есть
, то есть  . Рассмотрим многочлены:
. Рассмотрим многочлены: 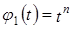 ,
, 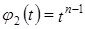 ,
, 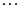 ,
, 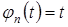 . Данная система многочленов линейно независима, так как включает многочлены разной степени и для любого многочлена подпространства M справедливо:
. Данная система многочленов линейно независима, так как включает многочлены разной степени и для любого многочлена подпространства M справедливо: 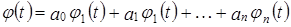 . Таким образом,
. Таким образом, 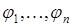 образует базис в M и dim M = n.
образует базис в M и dim M = n. .
. :
: 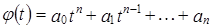 . Пусть
. Пусть 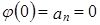 ,
, 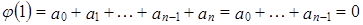 . Тогда
. Тогда 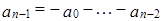 и многочлен имеет вид:
и многочлен имеет вид: 
 .
.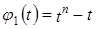 ,
,  ,
, 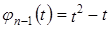 .
.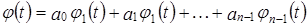 . Таким образом,
. Таким образом, 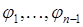 образует базис в M и dim M = n-1.
образует базис в M и dim M = n-1.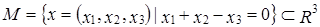
 . Тогда
. Тогда 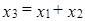 и
и  имеет вид:
имеет вид: 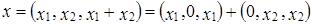 .
.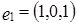 ,
, 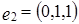 . Легко проверить, что векторы
. Легко проверить, что векторы 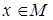 справедливо:
справедливо: 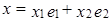 . Таким образом,
. Таким образом,  называется кососимметрической, если
называется кососимметрической, если 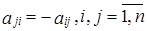 .
. , т.е. матрица
, т.е. матрица  имеет вид:
имеет вид: 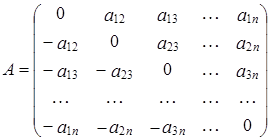 .
.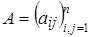 ,
, 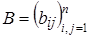 . Согласно определению,
. Согласно определению, 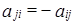 ,
, 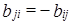 ,
, 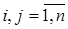 .
. . Элементы
. Элементы 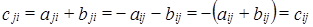 . Следовательно,
. Следовательно, 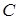 - кососимметрическая матрица.
- кососимметрическая матрица.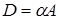 , где
, где 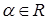 и
и 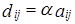 .Элементы
.Элементы  , т.е.
, т.е. 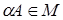 , и следовательно, M – линейное подпространство. Рассмотрим матрицы подпространства M:
, и следовательно, M – линейное подпространство. Рассмотрим матрицы подпространства M: 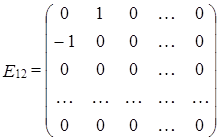 ,
, 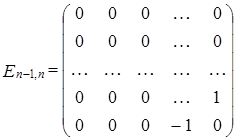 , где
, где 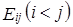 - матрица, у которой элемент
- матрица, у которой элемент  равен 1, элемент
равен 1, элемент 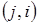 равен –1, а остальные элементы – нули. Число таких матриц
равен –1, а остальные элементы – нули. Число таких матриц 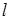 равно числу наддиагональных элементов матрицы размерности
равно числу наддиагональных элементов матрицы размерности  :
: 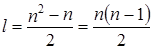 .
. линейно независимы и любая кососимметрическая матрица представима в виде их линейной комбинации:
линейно независимы и любая кососимметрическая матрица представима в виде их линейной комбинации: .
.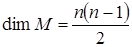 .
. и
и  , если каждый вектор
, если каждый вектор 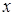 из X единственным образом можно представить в виде:
из X единственным образом можно представить в виде: 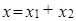 , где
, где  . Используется обозначение
. Используется обозначение  .
.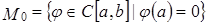 и подпространства постоянных функций
и подпространства постоянных функций  .
.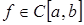 . Тогда справедливо представление:
. Тогда справедливо представление: 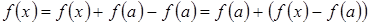 , где
, где  – константа, а функция
– константа, а функция 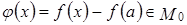 . Следовательно, любой элемент
. Следовательно, любой элемент 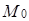 и
и 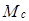 . Докажем, что такое представление единственно.
. Докажем, что такое представление единственно.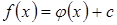 , где
, где 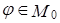 ,
, 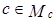 .
. ,
, 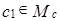 (
(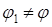 или (и)
или (и) 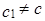 ) такие, что
) такие, что 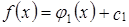 . Тогда
. Тогда 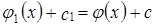 ,
, 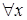 . Рассмотрим
. Рассмотрим  . Так как
. Так как 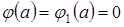 , то
, то 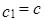 . Таким образом,
. Таким образом, 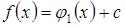 . Тогда
. Тогда 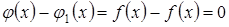 ,
, 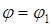 , что противоречит предположению.
, что противоречит предположению. .
.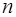 есть прямая сумма линейных подпространств
есть прямая сумма линейных подпространств 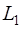 – симметрических матриц и
– симметрических матриц и 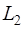 – кососимметрических матриц.
– кососимметрических матриц. – произвольная квадратная матрица. Покажем, что ее можно единственным образом представить в виде
– произвольная квадратная матрица. Покажем, что ее можно единственным образом представить в виде 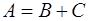 , где
, где 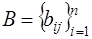 и
и 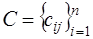 – симметрическая и кососимметрическая матрицы соответственно.
– симметрическая и кососимметрическая матрицы соответственно. , откуда
, откуда 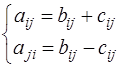 . Сложим первое и второе уравнения системы, получим
. Сложим первое и второе уравнения системы, получим 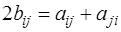 , откуда
, откуда 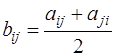 . Очевидно, что
. Очевидно, что 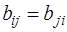 , то есть матрица
, то есть матрица  – симметрическая.
– симметрическая. , откуда
, откуда 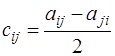 . Очевидно, что
. Очевидно, что 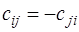 , то есть матрица
, то есть матрица 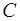 – кососимметрическая.
– кососимметрическая.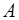 разложили на сумму симметрической и кососимметрической матриц, элементы которых определяются единственным образом, то есть пространство всех квадратных матриц порядка
разложили на сумму симметрической и кососимметрической матриц, элементы которых определяются единственным образом, то есть пространство всех квадратных матриц порядка 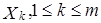 – совокупность линейных пространств, рассматриваемых над одним и тем же полем K. Их произведение
– совокупность линейных пространств, рассматриваемых над одним и тем же полем K. Их произведение 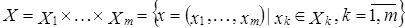 является линейным пространством, если для любой пары элементов
является линейным пространством, если для любой пары элементов 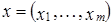 ,
, 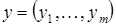 из X и числа
из X и числа  положить:
положить: 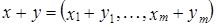 ,
, 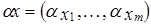 .
.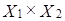 линейных пространств
линейных пространств 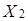 .
.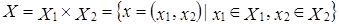 .
.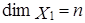 и
и  – базис в
– базис в  и
и  – базис в
– базис в 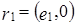 ,
, 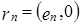 ,
, 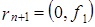 ,
,  . Докажем, что
. Докажем, что 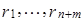 образуют базис в X.
образуют базис в X.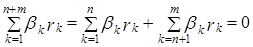

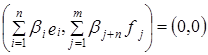
 , что в силу линейной независимости векторов
, что в силу линейной независимости векторов  . Таким образом, система векторов
. Таким образом, система векторов 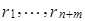 линейно независима.
линейно независима. ,
,  :
: 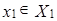 ,
, 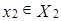 . Тогда
. Тогда 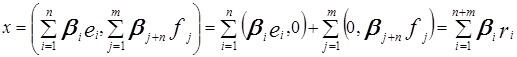 . Следовательно,
. Следовательно, 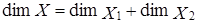 .
.


