Таким образом, если известно, что размерность пространства равна n, то для доказательства того факта, что система векторов является базисом, необходимо и достаточно доказать, что векторы системы линейно независимы.
Задача 9. В пространстве  заданы векторы
заданы векторы  ,
,  ,
,  ,
, 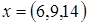 . Показать, что векторы
. Показать, что векторы  образуют базис и найти координаты вектора x в этом базисе.
образуют базис и найти координаты вектора x в этом базисе.
Решение.
1) Докажем, что  – базис в пространстве
– базис в пространстве  . Так как dim
. Так как dim  =3, то нам достаточно проверить линейную независимость векторов. Составим линейную комбинацию
=3, то нам достаточно проверить линейную независимость векторов. Составим линейную комбинацию  :
:



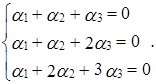
Определитель матрицы полученной системы 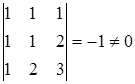 . Следовательно, система имеет только нулевое решение
. Следовательно, система имеет только нулевое решение  и векторы
и векторы  линейно независимы.
линейно независимы.
2. Для нахождения координат вектора x в базисе  составим равенство:
составим равенство: 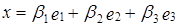

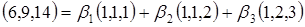 . Переходя к покоординатным равенствам и решая полученную систему, находим, что
. Переходя к покоординатным равенствам и решая полученную систему, находим, что  ,
,  ,
,  . Таким образом, в базисе
. Таким образом, в базисе  вектор
вектор 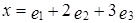 .
.
Задача 10. Пусть X – линейное пространство размерности n и  – векторы из X такие, что каждый вектор из X является их линейной комбинацией. Докажите, что эти векторы образуют базис в X.
– векторы из X такие, что каждый вектор из X является их линейной комбинацией. Докажите, что эти векторы образуют базис в X.
Решение.
Так как свойство 2) определения базиса выполнено по условию задачи, остается доказать линейную независимость векторов  , где n =dim X.
, где n =dim X.
Предположим противное. Пусть  – линейно зависимая система векторов. Выберем в M максимальную независимую подсистему векторов
– линейно зависимая система векторов. Выберем в M максимальную независимую подсистему векторов 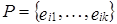 , k<n. Напомним, что конечная подсистема данной системы векторов называется максимальной линейно независимой, если сама подсистема векторов линейно независимая, а добавление к ней хотя бы одного вектора системы делают ее линейно зависимой. Каждый вектор системы линейно выражается через векторы ее максимальной независимой подсистемы, то есть,
, k<n. Напомним, что конечная подсистема данной системы векторов называется максимальной линейно независимой, если сама подсистема векторов линейно независимая, а добавление к ней хотя бы одного вектора системы делают ее линейно зависимой. Каждый вектор системы линейно выражается через векторы ее максимальной независимой подсистемы, то есть,  для любого
для любого 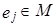 ,
, 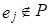 . Тогда для любого вектора x из линейного пространства X справедливо:
. Тогда для любого вектора x из линейного пространства X справедливо:
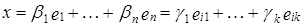 .
.
Таким образом, векторы 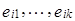 линейно независимы и любой элемент линейного пространства X представим в виде их линейной комбинации, т.е.
линейно независимы и любой элемент линейного пространства X представим в виде их линейной комбинации, т.е.  , что противоречит тому, что dim X=n.
, что противоречит тому, что dim X=n.
Задача 11. Докажите, что для любого комплексного числа a многочлены 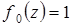 ,
, 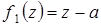 ,
,  , …,
, …, 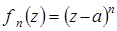 образуют базис в линейном пространстве
образуют базис в линейном пространстве  . Найти координаты произвольного многочлена в этом базисе.
. Найти координаты произвольного многочлена в этом базисе.
Решение.
Линейная независимость многочленов разной степени  следует из решения задачи 6. Докажем, что произвольный многочлен пространства
следует из решения задачи 6. Докажем, что произвольный многочлен пространства  является линейной комбинацией данных векторов.
является линейной комбинацией данных векторов.
Рассмотрим произвольный многочлен 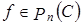 . Так как любой многочлен для любого
. Так как любой многочлен для любого 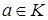 может быть единственным образом представлен в виде:
может быть единственным образом представлен в виде:
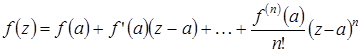 , то для любого
, то для любого 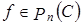 справедливо разложение по данной системе многочленов:
справедливо разложение по данной системе многочленов:
 .
.
Числа  являются координатами многочлена f в базисе
являются координатами многочлена f в базисе  .
.
Пусть X – произвольное линейное пространство. Для нахождения базиса 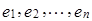 в пространстве X можно воспользоваться следующим алгоритмом.
в пространстве X можно воспользоваться следующим алгоритмом.
Алгоритм 1 (нахождение базиса в линейном пространстве).
5) Выбираем произвольный вектор  в пространстве X.
в пространстве X.
6) Если для любого вектора  существует
существует  такое, что справедливо представление:
такое, что справедливо представление:
 , (*)
, (*)
то останов. Размерность пространства X: dim X =1,  – базис в X.
– базис в X.
Иначе – находим произвольный вектор  , для которого не существует
, для которого не существует  такое, что выполняется равенство (*), то есть:
такое, что выполняется равенство (*), то есть:
,.
Полагаем  . Отметим, что векторы
. Отметим, что векторы 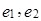 – линейно независимы в силу нарушения (*).
– линейно независимы в силу нарушения (*).
7) Если для любого вектора  существуют
существуют 
 такие, что:
такие, что:
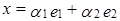 , (**)
, (**)
то останов, dim X =2; 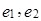 – базис в X.
– базис в X.
Иначе – находим вектор 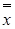 , для которого не выполнено равенство (**):
, для которого не выполнено равенство (**): 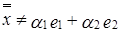 ,
,  .
.
Полагаем  ;
;  – линейно независимые векторы.
– линейно независимые векторы.
Продолжая данный процесс для конечномерного линейного пространства, через конечное число шагов алгоритма будет найден базис в пространстве X.
Задача 12. Систему многочленов  ,
, 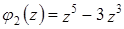 ,
,  ,
, 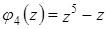 дополните до базиса пространства
дополните до базиса пространства  .
.
Решение.
Так как размерность пространства многочленов степени не выше 5:  равна 6, то необходимо найти многочлены
равна 6, то необходимо найти многочлены  , являющиеся линейно независимыми как между собой, так и с многочленами
, являющиеся линейно независимыми как между собой, так и с многочленами 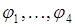 .
.
Найдем произвольный многочлен  , являющийся линейно независимым с системой
, являющийся линейно независимым с системой 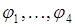 . Очевидно, что в качестве такого многочлена можно выбрать
. Очевидно, что в качестве такого многочлена можно выбрать 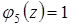 .
.
Для нахождения последнего многочлена базиса воспользуемся алгоритмом 1, т.е. найдем многочлен  , являющийся линейно независимым с системой
, являющийся линейно независимым с системой 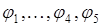 , т.е. для которого не существуют числа
, т.е. для которого не существуют числа 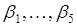 такие, что выполняется равенство:
такие, что выполняется равенство:


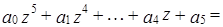
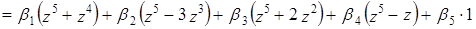


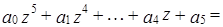


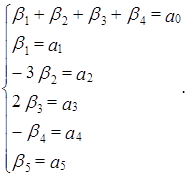
Неизвестными системы являются 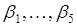 ;
;  - параметры системы. Система не имеет решения, например, для следующих значений параметров:
- параметры системы. Система не имеет решения, например, для следующих значений параметров: 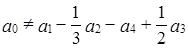 . Тогда в качестве базисного многочлена выберем
. Тогда в качестве базисного многочлена выберем 
 .
.
Система многочленов  линейно независима и образует базис в пространстве
линейно независима и образует базис в пространстве  .
.

 заданы векторы
заданы векторы  ,
,  ,
,  ,
, 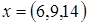 . Показать, что векторы
. Показать, что векторы  образуют базис и найти координаты вектора x в этом базисе.
образуют базис и найти координаты вектора x в этом базисе.

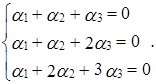
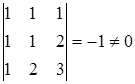 . Следовательно, система имеет только нулевое решение
. Следовательно, система имеет только нулевое решение  и векторы
и векторы 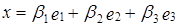
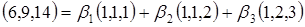 . Переходя к покоординатным равенствам и решая полученную систему, находим, что
. Переходя к покоординатным равенствам и решая полученную систему, находим, что  ,
,  ,
,  . Таким образом, в базисе
. Таким образом, в базисе 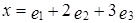 .
. – векторы из X такие, что каждый вектор из X является их линейной комбинацией. Докажите, что эти векторы образуют базис в X.
– векторы из X такие, что каждый вектор из X является их линейной комбинацией. Докажите, что эти векторы образуют базис в X. , где n =dim X.
, где n =dim X.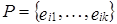 , k<n. Напомним, что конечная подсистема данной системы векторов называется максимальной линейно независимой, если сама подсистема векторов линейно независимая, а добавление к ней хотя бы одного вектора системы делают ее линейно зависимой. Каждый вектор системы линейно выражается через векторы ее максимальной независимой подсистемы, то есть,
, k<n. Напомним, что конечная подсистема данной системы векторов называется максимальной линейно независимой, если сама подсистема векторов линейно независимая, а добавление к ней хотя бы одного вектора системы делают ее линейно зависимой. Каждый вектор системы линейно выражается через векторы ее максимальной независимой подсистемы, то есть,  для любого
для любого 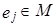 ,
, 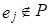 . Тогда для любого вектора x из линейного пространства X справедливо:
. Тогда для любого вектора x из линейного пространства X справедливо: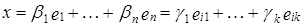 .
.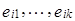 линейно независимы и любой элемент линейного пространства X представим в виде их линейной комбинации, т.е.
линейно независимы и любой элемент линейного пространства X представим в виде их линейной комбинации, т.е.  , что противоречит тому, что dim X=n.
, что противоречит тому, что dim X=n.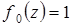 ,
, 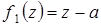 ,
,  , …,
, …, 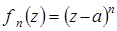 образуют базис в линейном пространстве
образуют базис в линейном пространстве  . Найти координаты произвольного многочлена в этом базисе.
. Найти координаты произвольного многочлена в этом базисе. следует из решения задачи 6. Докажем, что произвольный многочлен пространства
следует из решения задачи 6. Докажем, что произвольный многочлен пространства 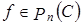 . Так как любой многочлен для любого
. Так как любой многочлен для любого 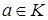 может быть единственным образом представлен в виде:
может быть единственным образом представлен в виде: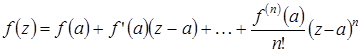 , то для любого
, то для любого  .
. являются координатами многочлена f в базисе
являются координатами многочлена f в базисе 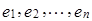 в пространстве X можно воспользоваться следующим алгоритмом.
в пространстве X можно воспользоваться следующим алгоритмом. в пространстве X.
в пространстве X. существует
существует  такое, что справедливо представление:
такое, что справедливо представление: , (*)
, (*) – базис в X.
– базис в X. , для которого не существует
, для которого не существует  такое, что выполняется равенство (*), то есть:
такое, что выполняется равенство (*), то есть: . Отметим, что векторы
. Отметим, что векторы 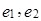 – линейно независимы в силу нарушения (*).
– линейно независимы в силу нарушения (*).
 такие, что:
такие, что: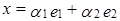 , (**)
, (**)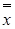 , для которого не выполнено равенство (**):
, для которого не выполнено равенство (**): 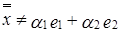 ,
,  .
. ;
;  ,
, 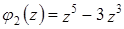 ,
,  ,
, 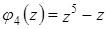 дополните до базиса пространства
дополните до базиса пространства  .
. , являющиеся линейно независимыми как между собой, так и с многочленами
, являющиеся линейно независимыми как между собой, так и с многочленами 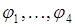 .
. , являющийся линейно независимым с системой
, являющийся линейно независимым с системой 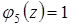 .
.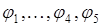 , т.е. для которого не существуют числа
, т.е. для которого не существуют числа 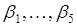 такие, что выполняется равенство:
такие, что выполняется равенство:
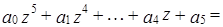
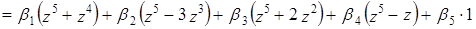

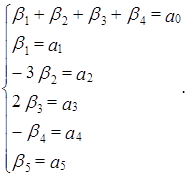
 - параметры системы. Система не имеет решения, например, для следующих значений параметров:
- параметры системы. Система не имеет решения, например, для следующих значений параметров: 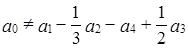 . Тогда в качестве базисного многочлена выберем
. Тогда в качестве базисного многочлена выберем 
 .
. линейно независима и образует базис в пространстве
линейно независима и образует базис в пространстве 


