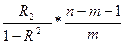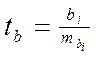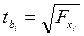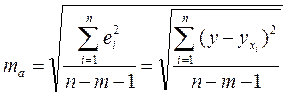Дисперсионный анализ. 1. Выдвигаем нулевую гипотезу:
1. Выдвигаем нулевую гипотезу: Н0=b1= b2= b3=…= bn=0 2. Наблюдаемое значение F-критерия Фишера (Fнабл) определяется по формуле:
Fнабл= Воспользуемся теоремой о разложении дисперсий:
TSS=RSS+ESS
Число степеней свободы: df для CКОобщ = n-1 df для CКОфакт= k1= m df для CКОост = k2=n-m-1 Схема дисперсионного анализа (см.парную регрессию) 3. Fтабл (α, k1, k2) 4. Сравниваем наблюдаемое и табличное значения. Делаем вывод: Если Fнабл> Fтабл, то нулевая гипотеза отклоняется и делается вывод о том, что коэффициенты уравнения множественной регрессии не равны 0, следовательно уравнение регрессии статистически значимо. Если Fнабл<Fтабл, то нулевая гипотеза отклоняется и делается вывод о том, что коэффициенты уравнения множественной регрессии равны 0, следовательно уравнение регрессии статистически незначимо. Оценка уравнения регрессии в целом может проводиться на основе множественного коэффициента детерминации:
Оценка параметров уравнения
Н0=a=0, Н0= b1= b2= b3=…= bn=0
2. или
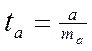
3. Находим tтабл (α,k2)
4.Сравниваем tнабл и tтабл. Если |ta, tb|> tтабл, то нулевая гипотеза отклоняется, коэффициенты уравнения регрессии не равны 0, следовательно статистически значимы. Если наоборот, то равны 0 и незначимы.
5.Доверительные интервалы: a (b)-ma(mb)* tтабл ≤a(b)≤ a (b)+ma(mb)* tтабл
|


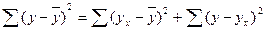
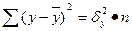
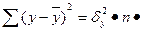 R2
R2
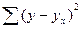 =CКОобщ-СКОфакт
=CКОобщ-СКОфакт
 =0
=0