На підставі (5.3) рівняння (5.4) запишемо у вигляді
s 23 dl = s 12 dl + s 13 dl cos q, або s 23= s 12+ s 13cos q, (5.5) звідки
Якщо σ;23< σ;12 і │ σ;23– σ;12│< σ;13, то Коефіцієнт поверхневого натягу залежить від різновиду рідини і середовища, з яким вона контактує. Для більшості рідин з підвищенням температури σ; лінійно зменшується, а за критичної температури σ= 0. Наближену залежність σ;= f (T)для температур Т < Т к дає емпірично визначене рівняння
де а – стала, Т к – критична температура; r – невелика поправка в розмірності температури; ρ; – густина; М – молярна маса рідини. Як бачимо, коефіцієнт поверхневого натягу лінійно зменшується з підвищенням температури. В довідниках, як звичайно, наведене значення σ; за кімнатної температури, коли рідина межує зі своєю парою.
Розглянемо сферичну краплину рідини, умовно перерізавши її площиною на дві половини, розмежовані колом радіуса R (рис. 5.5). На кожен елемент довжини кола Δ l діятимуть сили поверхневого натягу fi = σ;Δ li вздовж дотичних до поверхні сфери. Сума цих сил дає рівнодійну f, яка перпендикулярна до площини перерізу:
Тоді тиск, зумовлений дією сили f,
де S – площа перерізу сферичної краплини. Якщо поверхня рідини відрізняється від сферичної, то кривину її поверхні описують через усереднений радіус кривини R с:
де r 1 і r 2 – радіуси кривизни поверхні у двох взаємноперпендикулярних площинах, що проходять через нормаль до поверхні. Радіус кривизни r додатний, якщо центр кривизни міститься всередині рідини і від’ємний, якщо центр кривини міститься поза нею. Для такої поверхні
Вираз (5.11) називають формулою Лапласа для додаткового тиску, зумовленого кривиною поверхні рідини. Сили додаткового тиску завжди напрямлені до центра кривини поверхні. Для сферичних поверхонь r 1= r 2= R і вираз (5.11) перетворюється у (5.9). Для циліндричної поверхні r 1 = R, а r 2=∞, тоді р д= За умови плоскої поверхні r 1= r 2=∞, отже, р д=0. Під плоскою поверхнею рідини додаткового тиску нема.
Під увігнутою поверхнею рідини (А) виникає від’ємний додатковий тиск p ц=2σ/ R. Дія сил додаткового тиску спричинює підняття рівня рідини в капілярі на висоту h, за якої гідростатичний тиск ρgh зрівноважить додатковий. Справді, згідно з законом Паскаля, тиски в точках 1 і 2 (рис. 5.6) однакові: p 1= p 2. Проте, p 1= p 0+ rg (l + h)+ p м– де р м – молекулярний тиск; р 0 – атмосферний тиск. Тоді p 0+ r g(l + h)+ p м – звідки ρgh =2 σ;/ R, (5.13) де ρ; – густина рідини; g – прискорення вільного падіння. Якщо змочування неповне, то R = r /cos θ;, (5.14) де R – радіус кривини меніска; r – радіус капіляра; θ – крайовий кут. Тоді (5.13) зведемо до вигляду
звідки
Вираз (5.16) дає змогу обчислити висоту підняття рідини в капілярі над рівнем рідини в посудині. За умови змочування (π;/2< θ;< π;/2, cos θ;>0) отримаємо додатні значення h, тоді як у разі незмочування (π;/2< θ;< π;, cos θ;<0) h буде від’ємним. Обчислимо тепер висоту піднімання рідини в циліндричному капілярі (дві паралельні пластини, відстань між якими d ~ R). Умову рівноваги стовпа рідини за цих умов запишемо у вигляді
Тоді
Явища, зумовлені поверхневим натягом рідин відіграють важливу роль у природі й техніці. Зокрема, вони пояснюють піднімання води з ґрунту по стовбурах дерев, дію фільтрувального паперу, збагачення руд флотацією, дію ефективних мийних засобів тощо.
|

 . (5.6)
. (5.6) Якщо σ;23> σ;12 і │ σ;23– σ;12│< σ;13, то крайовий кут 0< θ;<π/2, оскільки 0<cos θ;<1. За умови 0< θ;<π/2 рідина частково змочує поверхню. Якщо ж q =0, то рідина повністю змочує поверхню, розтікаючись по ній молекулярним шаром.
Якщо σ;23> σ;12 і │ σ;23– σ;12│< σ;13, то крайовий кут 0< θ;<π/2, оскільки 0<cos θ;<1. За умови 0< θ;<π/2 рідина частково змочує поверхню. Якщо ж q =0, то рідина повністю змочує поверхню, розтікаючись по ній молекулярним шаром.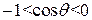 і крайовий кут π/2< θ;<π. Це умова незмочування рідиною поверхні стінки посудини. Умови змочування і незмо-чування зумовлюють різну форму поверхні рідини біля стінки посудини (рис. 5.3).
і крайовий кут π/2< θ;<π. Це умова незмочування рідиною поверхні стінки посудини. Умови змочування і незмо-чування зумовлюють різну форму поверхні рідини біля стінки посудини (рис. 5.3). (5.7)
(5.7)
 Якщо поверхня рідини не є плоскою, то сили поверхневого натягу зумовлюють виникнення додаткового тиску під викривленою поверхнею рідини. Переконатись у наявності додаткового тиску, зумовленого кривизною поверхні рідини, можна, виконавши нескладний експеримент з мильними бульбашками. Якщо на кінцях скляної трубки (рис. 5.4) видути бульбашки А і В різного діаметра і полишити систему саму на себе, то можна спостерігати, що бульбашка В меншого діаметра завжди зменшу-ватиметься, а буль-башка А більшого діаметра збільшуватиметься. Отже, тиск усе-редині В більший, ніж тиск усередині А, радіус кривини поверхні якої є більшим.
Якщо поверхня рідини не є плоскою, то сили поверхневого натягу зумовлюють виникнення додаткового тиску під викривленою поверхнею рідини. Переконатись у наявності додаткового тиску, зумовленого кривизною поверхні рідини, можна, виконавши нескладний експеримент з мильними бульбашками. Якщо на кінцях скляної трубки (рис. 5.4) видути бульбашки А і В різного діаметра і полишити систему саму на себе, то можна спостерігати, що бульбашка В меншого діаметра завжди зменшу-ватиметься, а буль-башка А більшого діаметра збільшуватиметься. Отже, тиск усе-редині В більший, ніж тиск усередині А, радіус кривини поверхні якої є більшим. s ×2 pR. (5.8)
s ×2 pR. (5.8)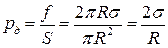 , (5.9)
, (5.9) , (5.10)
, (5.10) . (5.11)
. (5.11) . (5.12)
. (5.12)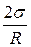 , a p 2= p 0+ rgl + p м,
, a p 2= p 0+ rgl + p м, , (5.15)
, (5.15)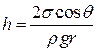 . (5.16)
. (5.16)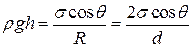 . (5.17)
. (5.17)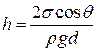 . (5.18)
. (5.18)


