Ентропія
Під час розгляду першого закону термодинаміки (3.1) ми виявили, що лише зміна внутрішньої енергії dU є повним диференціалом. Це зумовлено тим, що внутрішня енергія – це функція стану термодинамічної системи, яка не залежить від способу переходу системи зі стану 1 у стан 2. Крім того, термодинаміка оперує іншими термодинамічними функціями, які є функціями стану системи. Одна з них – ентропія S. Спробуємо, скориставшись (3.1) та (3.12), виділити один повний диференціал функції, що залежить від макропараметрів ідеального газу:
Поділимо (3.51) на Т, отримаємо
Як бачимо, праворуч у рівнянні (3.52) маємо повний диференціал, отже, і ліва частина рівняння повинна бути повним диференціалом. Функцію стану, повним диференціалом якої є
Фізичний зміст ентропії виражає формула Больцмана S=к·lnW, (3.54) де W – термодинамічна ймовірність. Термодинамічна ймовірність W – це кількість мікростанів, які зумовлюють заданий макростан системи. На відміну від математичної ймовірності, яка не може бути більшою від одиниці, W може набувати будь-яких додатних значень. Отже, ентропія S визначена логарифмом кількості мікростанів системи, за допомогою яких може бути реалізовано цей мікростан. Ентропія має ще й статистичне тлумачення – вона є мірою розупорядкованості системи. Справді, зі збільшенням упорядкованості частинок системи кількість мікростанів зменшується, отже, зменшується й ентропія. Якщо система перебуває в стані термодинамічної рівноваги, то кількість мікростанів максимальна, отже, максимальною є ентропія системи. З урахуванням ентропії рівняння (3.51) для оборотних процесів можна записати так:
Це головна термодинамічна тотожність. Для характеристики різноманітних термодинамічних процесів важли-вою є не ентропія системи, а її зміна. Щоб обчислити зміну ентропії у певному процесі, скористаємось (3.55):
1. Ізотермічний процес:
2. Ізохорний процес:
3. Ізобарний процес:
однак
4. Адіабатний процес: Δ S =0, оскільки δQ =0. Отже, адіабатний процес є ізоентропійним. Зміна ентропії в необоротних процесах. Розглянемо зміну ентропії під час вирівнювання температури двох тіл, які перебувають у тепловому контакті. Нехай температура першого тіла Т 1, а другого – Т 2. Після контакту температура обох тіл Т 3. Щоб визначити цю температуру скористаємось рівнянням теплового балансу
звідки
Тут m i c – маса і питома теплоємність кожного тіла. Зміну ентропії в цьому нерівноважному процесі можна обчислити, звівши його до двох рівноважних процесів. Тоді
звідки
Підставимо у (3.62) і (3.63), і переконаємось, що Δ S >0, тобто під час теплопередавання ентропія зростає. Необоротними є також фазові переходи першого роду. Під час таких процесів зміну ентропії системи виражає формула
де q – питома теплота; Т – температура фазового переходу.
|

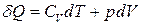 . (3.51)
. (3.51) . (3.52)
. (3.52)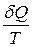 , називають ентропією S, отже,
, називають ентропією S, отже, . (3.53)
. (3.53) . (3.55)
. (3.55) . (3.56)
. (3.56)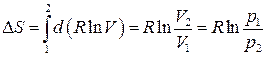 . (3.57)
. (3.57) . (3.58)
. (3.58) , (3.59)
, (3.59) , тоді
, тоді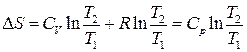 . (3.60)
. (3.60)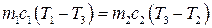 , (3.61)
, (3.61) . (3.62)
. (3.62)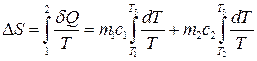 ,
, , (3.63)
, (3.63) , (3.64)
, (3.64)


