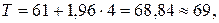1) 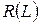 – резерв времени пути определяется как разность между длиной критического пути и длиной рассматриваемого пути:
– резерв времени пути определяется как разность между длиной критического пути и длиной рассматриваемого пути:
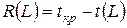 . (6)
. (6)
Например, для пути  этот резерв равен
этот резерв равен
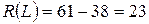 .
.
То есть продолжительность работ на этом пути можно суммарно увеличить на 23 дня. Другими словами, любая из работ, не принадлежащих критическому пути, обладает резервом времени.
2) 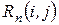 – полный резерв времени работы
– полный резерв времени работы 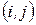 вычисляется по формуле:
вычисляется по формуле:
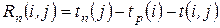 , (7)
, (7)
и показывает, на сколько дней можно увеличить время выполнения данной работы, если срок выполнения всего комплекса работ не изменится. Проиллюстрируем (7) на следующем рисунке:
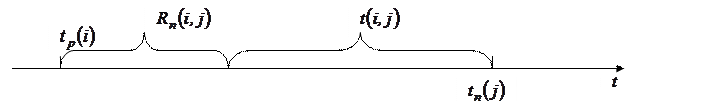
Рис. 6.
3) 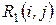 – частный резерв времени первого вида работы
– частный резерв времени первого вида работы  – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока наступления события
– это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока наступления события 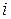 :
:
 , (8)
, (8)
или
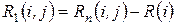 . (8’)
. (8’)
Проиллюстрируем:
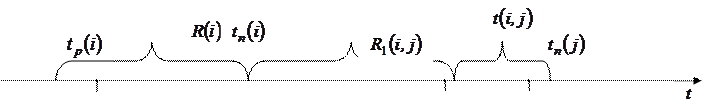
Рис. 7.
4) 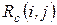 частный (или свободный) резерв времени второго вида – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока наступления события
частный (или свободный) резерв времени второго вида – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока наступления события 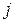 :
:
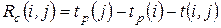 , (9)
, (9)
или
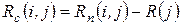 . (9¢)
. (9¢)
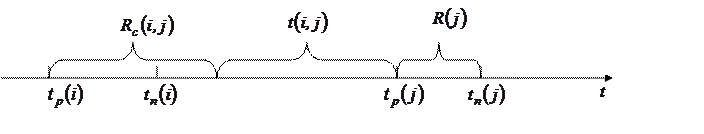
Рис. 8.
5)  независимый резерв времени работы
независимый резерв времени работы 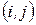 – это часть полного резерва времени, когда событие
– это часть полного резерва времени, когда событие 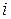 начинается в позднее время, а
начинается в позднее время, а 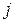 начинается в раннее время:
начинается в раннее время:
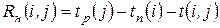 , (10)
, (10)
или
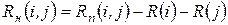 . (10’)
. (10’)
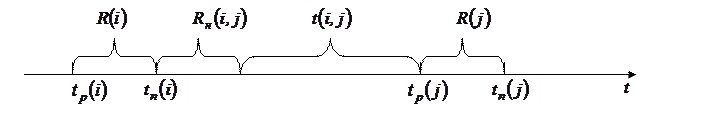
Рис. 9.
Отметим, что отрицательное 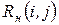 смысла не имеет.
смысла не имеет.
Таким образом:
а) 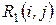 может быть использован на увеличение продолжительности данной и последующих работ, без затрат резерва времени предшествующих работ.
может быть использован на увеличение продолжительности данной и последующих работ, без затрат резерва времени предшествующих работ.
б) 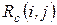 – на увеличение продолжительности данной и предшествующих работ без нарушения резерва времени последующих работ.
– на увеличение продолжительности данной и предшествующих работ без нарушения резерва времени последующих работ.
в) 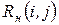 – на увеличение продолжительности только данной работы.
– на увеличение продолжительности только данной работы.
Следует отметить, что:
1) Работы, лежащие на критическом пути, резервов времени не имеют.
2) Если на критическом пути лежит начальное событие 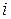 , то
, то
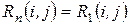 .
.
3) Если – конечное событие 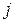 , то
, то
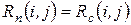 .
.
4) Если и 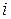 и
и 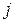 лежат на критическом пути, но сама работа
лежат на критическом пути, но сама работа 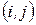 не принадлежит этому пути, то
не принадлежит этому пути, то
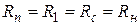 . (11)
. (11)
Вычислим временные параметры работ для данного сетевого графика.
Таблица 2.
| №
n/n
| Работа 
| Продолжи-тельность работы 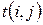
| Сроки начала и окончания работы
| Резервы времени работы
|
| 
| 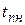
| 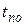
| 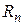
| 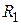
| 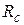
| 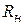
|
|
| (0,1)
|
|
|
|
|
|
|
|
|
|
|
| (0,3)
|
|
|
|
|
|
|
|
|
|
|
| (0,5)
|
|
|
|
|
|
|
|
|
|
|
| (1,2)
|
|
|
|
|
|
|
|
| -
|
|
| (1,3)
|
|
|
|
|
|
|
|
|
|
|
| (1,4)
|
|
|
|
|
|
|
|
|
|
|
| (2,7)
|
|
|
|
|
|
|
|
| -
|
|
| (3,4)
|
|
|
|
|
|
|
|
|
|
|
| (3,5)
|
|
|
|
|
|
|
|
|
|
|
| (3,6)
|
|
|
|
|
|
|
|
|
|
|
| (4,6)
|
|
|
|
|
|
|
|
|
|
|
| (4,7)
|
|
|
|
|
|
|
|
| -
|
|
| (5,6)
|
|
|
|
|
|
|
|
|
|
|
| (5,8)
|
|
|
|
|
|
|
|
|
|
|
| (5,9)
|
|
|
|
|
|
|
|
|
|
|
| (6,7)
|
|
|
|
|
|
|
|
|
|
|
| (6,8)
|
|
|
|
|
|
|
|
|
|
|
| (6,9)
|
|
|
|
|
|
|
|
|
|
|
| (6,10)
|
|
|
|
|
|
|
|
|
|
|
| (7,10)
|
|
|
|
|
|
|
|
|
|
|
| (8,9)
|
|
|
|
|
|
|
|
|
|
|
| (9,10)
|
|
|
|
|
|
|
|
|
|
|
| (9,11)
|
|
|
|
|
|
|
|
|
|
|
| (10,11)
|
|
|
|
|
|
|
|
|
|
Сделаем небольшие пояснения к этой таблице, на примере работы (1,4) так как для нее все резервы работы разные.
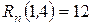 означает, что резерв максимального из путей, проходящих через работу (1,4) равен 12 дням, после чего он станет (если добавить 12 дней к работе (1,4)) критическим. Резервы времени остальных путей, проходящих через работу (1,4) уменьшатся на эти же 12 дней.
означает, что резерв максимального из путей, проходящих через работу (1,4) равен 12 дням, после чего он станет (если добавить 12 дней к работе (1,4)) критическим. Резервы времени остальных путей, проходящих через работу (1,4) уменьшатся на эти же 12 дней.
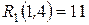 означает, что на 11 дней может быть задержано выполнение работы (1,4) и всех последующих работ по любому пути, проходящему через (1,4) без изменения резерва времени предшествующих работ.
означает, что на 11 дней может быть задержано выполнение работы (1,4) и всех последующих работ по любому пути, проходящему через (1,4) без изменения резерва времени предшествующих работ.
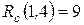 означает, что на 9 дней может быть задержано выполнение работы (1,4) и предшествующих ей работ, без изменения резерва времени последующих работ.
означает, что на 9 дней может быть задержано выполнение работы (1,4) и предшествующих ей работ, без изменения резерва времени последующих работ.
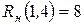 означает, что на 8 дней можно задержать выполнение работы (1,4) без изменения резервов времени остальных работ.
означает, что на 8 дней можно задержать выполнение работы (1,4) без изменения резервов времени остальных работ.
Видно из таблицы, что резервы критических работ равны нулю, что естественно. Кроме того, если  , то в соответствующей клетке ставим прочерк.
, то в соответствующей клетке ставим прочерк.
СЕТЕВОЕ ПЛАНИРОВАНИЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Выше предполагалось, что время выполнения каждой работы известно точно. Однако на практике это не так, то есть время 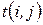 является случайной величиной.
является случайной величиной.
Анализ большого количества статистических данных показал, что 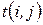 имеет приближенно так называемое
имеет приближенно так называемое 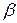 -распределение. И априори предполагается, что закон распределения случайной величины задается функцией плотности распределения вероятностей, обладающей следующими свойствами:
-распределение. И априори предполагается, что закон распределения случайной величины задается функцией плотности распределения вероятностей, обладающей следующими свойствами:
1) непрерывность;
2) унимодальность, то есть функция плотности распределения имеет единственный максимум;
3) двумя точками пересечения с временной осью с положительной абсциссой;
4) положительной асимметрией.
Таким образом, плотности распределения вероятностей случайной величины 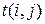 может выглядеть как
может выглядеть как
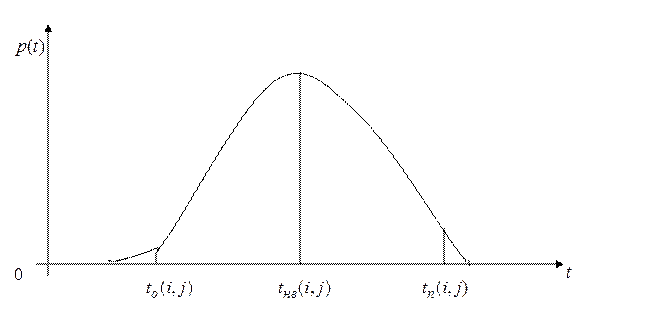
Рис.10.
Для вычисления числовых характеристик – математического ожидания ( ) и дисперсии (
) и дисперсии (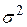 ), а точнее их оценок, используют экспертные оценки:
), а точнее их оценок, используют экспертные оценки:
1) 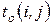 - оптимистичную оценку продолжительности работ при самых благоприятных условиях.
- оптимистичную оценку продолжительности работ при самых благоприятных условиях.
2) 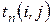 - пессимистическую оценку – при самых неблагоприятных условиях.
- пессимистическую оценку – при самых неблагоприятных условиях.
3) 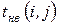 - наиболее вероятную оценку – при «нормальных» условиях. (см. рис.10)
- наиболее вероятную оценку – при «нормальных» условиях. (см. рис.10)
Тогда оценку математического ожидания можно вычислить по формулам:
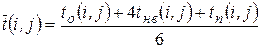 , (12)
, (12)
или
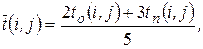 (12’)
(12’)
так как на практике наиболее тяжело оценить именно 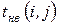 .
.
А оценка дисперсии имеет вид
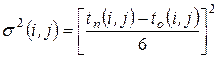 . (13)
. (13)
Если путь 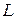 содержит большее количество работ, то общая продолжительность пути
содержит большее количество работ, то общая продолжительность пути  будет представлять собой сумму большего количества случайных величин и при некоторых, весьма общих условиях, будет удовлетворять условиям центральной предельной теоремы Ляпунова. То есть
будет представлять собой сумму большего количества случайных величин и при некоторых, весьма общих условиях, будет удовлетворять условиям центральной предельной теоремы Ляпунова. То есть  будет иметь асимптотически нормальное распределение с параметрами:
будет иметь асимптотически нормальное распределение с параметрами:
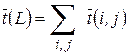 ,
, 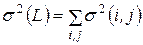 . (14)
. (14)
Таким образом, для анализа продолжительности пути  можно использовать соответствующие формулы нормального распределения, считая, что все параметры, вычисленные нами ранее, являются средними значениями соответствующих случайных величин. Например,
можно использовать соответствующие формулы нормального распределения, считая, что все параметры, вычисленные нами ранее, являются средними значениями соответствующих случайных величин. Например, 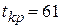 означает, что длина критического пути равна 61 лишь «в среднем», а на практике возможны отклонения от этого значения: тем большие, чем больше дисперсия
означает, что длина критического пути равна 61 лишь «в среднем», а на практике возможны отклонения от этого значения: тем большие, чем больше дисперсия 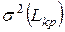 .
.
Поэтому после расчета временных параметров сети (§5) можно решать следующие задачи оценки параметров, такие как:
1. Оценка вероятности того, что срок выполнения проекта не превысит некоторого значения 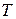 :
:
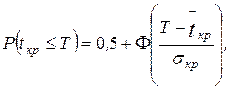 (15)
(15)
где  - функция Лапласа, а
- функция Лапласа, а 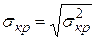 - выборочное среднее квадратическое отклонение.
- выборочное среднее квадратическое отклонение.
2. Оценка максимального срока выполнения проекта с заданной надежностью 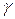 :
:
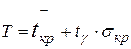 , (16)
, (16)
где 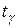 ищется по таблице значений функции Лапласа, согласно условию
ищется по таблице значений функции Лапласа, согласно условию 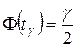 .
.
Пусть, например, для рассматриваемого примера известны дисперсии работ критического пути:
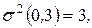
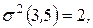
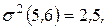
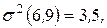
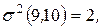
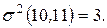
Тогда оценки критического пути будут равны:
 ,
, 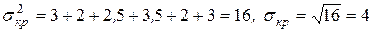 .
.
Оценим теперь вероятность того, что срок выполнения проекта не превысит 64 дня по формуле (15):
 , или
, или 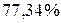 .
.
Оценим также и максимально возможный срок выполнения проекта с надежностью 0,95 по формуле (16):
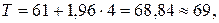
то есть с надежностью в 95% можно утверждать, что срок выполнения проекта не превысит 69 дней.
Следует отметить, что получаемые результаты являются весьма приближенными, хотя и позволяют получать некоторые оценки «в первом приближении». Дело в том, что:
1. Теорема Ляпунова дает хорошее приближение нормальным распределениям лишь при большом числе работ в цепи.
2. Даже при большом числе работ дисперсии длин некритических путей могут оказаться гораздо больше дисперсии критического пути, что может привести к тому (при изменении некоторых условий), что критическим станет другой путь.
Неопределенность в сетевом планировании и управлении может быть определена не только случайным характером продолжительности выполнения работ, но и со случайностью в выполнении работ и целых комплексов работ. Например, строить крупное, мелкое или среднее предприятие по переработке полезных ископаемых или просто продать лицензию – зависит от объемов разведанного сырья. Такие сети называются стохастическими.
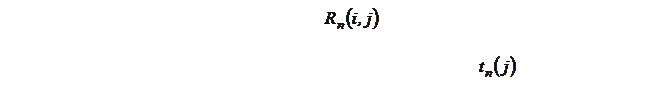

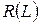 – резерв времени пути определяется как разность между длиной критического пути и длиной рассматриваемого пути:
– резерв времени пути определяется как разность между длиной критического пути и длиной рассматриваемого пути: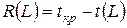 . (6)
. (6)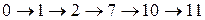 этот резерв равен
этот резерв равен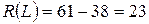 .
. – полный резерв времени работы
– полный резерв времени работы  вычисляется по формуле:
вычисляется по формуле: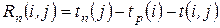 , (7)
, (7)

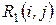 – частный резерв времени первого вида работы
– частный резерв времени первого вида работы  – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока наступления события
– это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока наступления события 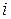 :
: , (8)
, (8)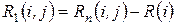 . (8’)
. (8’)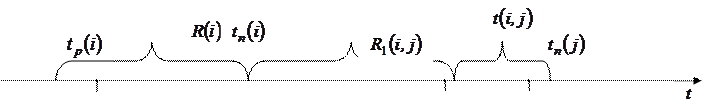
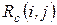 частный (или свободный) резерв времени второго вида – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока наступления события
частный (или свободный) резерв времени второго вида – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока наступления события 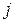 :
: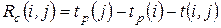 , (9)
, (9)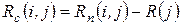 . (9¢)
. (9¢)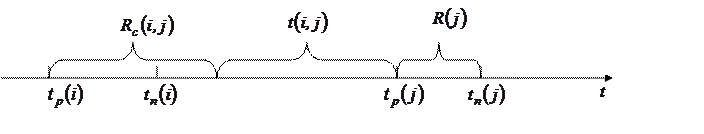
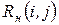 независимый резерв времени работы
независимый резерв времени работы 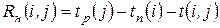 , (10)
, (10)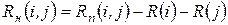 . (10’)
. (10’)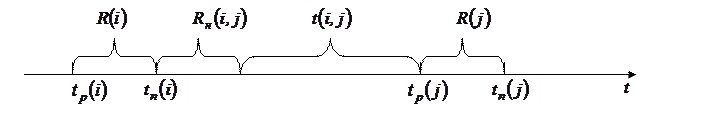
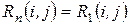 .
.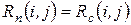 .
.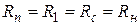 . (11)
. (11)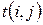
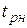

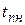
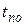
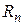
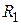
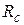
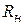
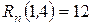 означает, что резерв максимального из путей, проходящих через работу (1,4) равен 12 дням, после чего он станет (если добавить 12 дней к работе (1,4)) критическим. Резервы времени остальных путей, проходящих через работу (1,4) уменьшатся на эти же 12 дней.
означает, что резерв максимального из путей, проходящих через работу (1,4) равен 12 дням, после чего он станет (если добавить 12 дней к работе (1,4)) критическим. Резервы времени остальных путей, проходящих через работу (1,4) уменьшатся на эти же 12 дней.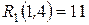 означает, что на 11 дней может быть задержано выполнение работы (1,4) и всех последующих работ по любому пути, проходящему через (1,4) без изменения резерва времени предшествующих работ.
означает, что на 11 дней может быть задержано выполнение работы (1,4) и всех последующих работ по любому пути, проходящему через (1,4) без изменения резерва времени предшествующих работ.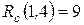 означает, что на 9 дней может быть задержано выполнение работы (1,4) и предшествующих ей работ, без изменения резерва времени последующих работ.
означает, что на 9 дней может быть задержано выполнение работы (1,4) и предшествующих ей работ, без изменения резерва времени последующих работ.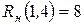 означает, что на 8 дней можно задержать выполнение работы (1,4) без изменения резервов времени остальных работ.
означает, что на 8 дней можно задержать выполнение работы (1,4) без изменения резервов времени остальных работ. , то в соответствующей клетке ставим прочерк.
, то в соответствующей клетке ставим прочерк.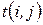 является случайной величиной.
является случайной величиной.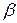 -распределение. И априори предполагается, что закон распределения случайной величины задается функцией плотности распределения вероятностей, обладающей следующими свойствами:
-распределение. И априори предполагается, что закон распределения случайной величины задается функцией плотности распределения вероятностей, обладающей следующими свойствами: может выглядеть как
может выглядеть как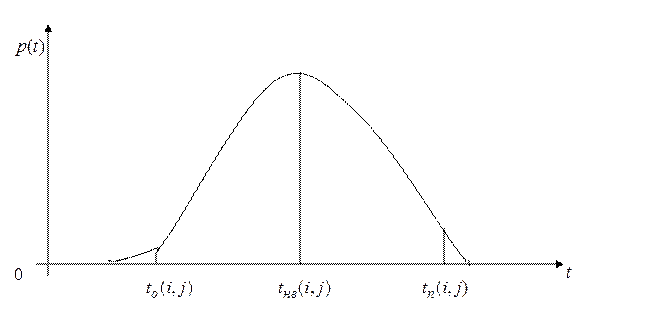
 ) и дисперсии (
) и дисперсии (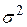 ), а точнее их оценок, используют экспертные оценки:
), а точнее их оценок, используют экспертные оценки: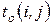 - оптимистичную оценку продолжительности работ при самых благоприятных условиях.
- оптимистичную оценку продолжительности работ при самых благоприятных условиях.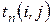 - пессимистическую оценку – при самых неблагоприятных условиях.
- пессимистическую оценку – при самых неблагоприятных условиях.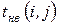 - наиболее вероятную оценку – при «нормальных» условиях. (см. рис.10)
- наиболее вероятную оценку – при «нормальных» условиях. (см. рис.10)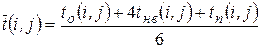 , (12)
, (12)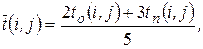 (12’)
(12’)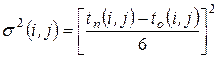 . (13)
. (13) содержит большее количество работ, то общая продолжительность пути
содержит большее количество работ, то общая продолжительность пути  будет представлять собой сумму большего количества случайных величин и при некоторых, весьма общих условиях, будет удовлетворять условиям центральной предельной теоремы Ляпунова. То есть
будет представлять собой сумму большего количества случайных величин и при некоторых, весьма общих условиях, будет удовлетворять условиям центральной предельной теоремы Ляпунова. То есть 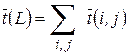 ,
, 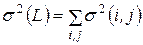 . (14)
. (14)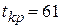 означает, что длина критического пути равна 61 лишь «в среднем», а на практике возможны отклонения от этого значения: тем большие, чем больше дисперсия
означает, что длина критического пути равна 61 лишь «в среднем», а на практике возможны отклонения от этого значения: тем большие, чем больше дисперсия 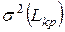 .
.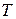 :
: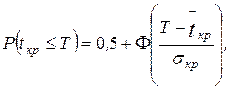 (15)
(15) - функция Лапласа, а
- функция Лапласа, а 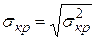 - выборочное среднее квадратическое отклонение.
- выборочное среднее квадратическое отклонение. :
: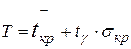 , (16)
, (16)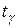 ищется по таблице значений функции Лапласа, согласно условию
ищется по таблице значений функции Лапласа, согласно условию 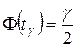 .
.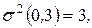
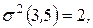
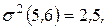
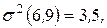
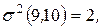
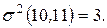
 ,
, 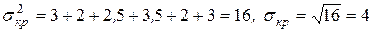 .
. , или
, или 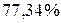 .
.