Зависимость между стоимостью и продолжительностью выполнения работ
Рассмотрим теперь сетевые графики, которые кроме продолжительности работ, характеризуются еще и стоимостью. То есть каждая работа
где
где Зависимость между стоимостью и продолжительностью работ можно проиллюстрировать графически:
Рис.11.
Решаются, в зависимости от принятого критерия оптимальности, триоптимизационные задачи: 1) Минимизация времени выполнения работ при заданной максимальной стоимости работ. 2) Минимизация стоимости работ при заданном сроке (максимально возможном) выполнения работ. 3) Нахождение оптимального соотношения величин стоимости и сроков работ, в зависимости от конкретных целей, поставленных при реализации соответствующего проекта (Парето - оптимальность). Если аппроксимировать зависимость стоимости от времени прямой (см. рис.11), то можно приближенно найти изменение стоимости работ
где
то есть
И если продолжительность каждой работы увеличить с
Отметим, что если речь идет о минимизации стоимости проекта, то продолжительность каждой работы целесообразно увеличить на величину свободного резерва времени
|

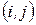 характеризуется продолжительностью:
характеризуется продолжительностью: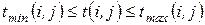 , (18)
, (18)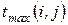 - нормальная продолжительность работ,
- нормальная продолжительность работ, 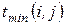 - экстренная, минимально возможная продолжительность работ. Стоимость
- экстренная, минимально возможная продолжительность работ. Стоимость 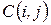 работы
работы 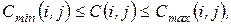 (19)
(19)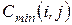 - стоимость работ при нормальной продолжительности, а
- стоимость работ при нормальной продолжительности, а 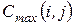 - при экстренной продолжительности.
- при экстренной продолжительности.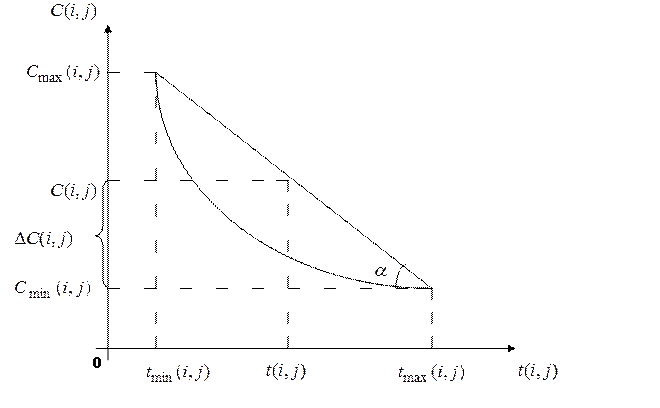
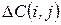 при сокращении продолжительности работ с
при сокращении продолжительности работ с 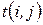 (или увеличение продолжительности работ с
(или увеличение продолжительности работ с  ):
):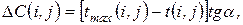
 называют затратами на ускорение работы
называют затратами на ускорение работы 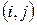 , по сравнению с нормальной продолжительностью, в расчете на одну единицу времени:
, по сравнению с нормальной продолжительностью, в расчете на одну единицу времени: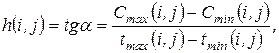 (20)
(20) (21)
(21)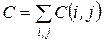 уменьшится на величину:
уменьшится на величину: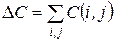 .
.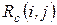 (это не относится к работам, расположенным на критическом пути, у них
(это не относится к работам, расположенным на критическом пути, у них  ).
).


