Решим теперь задачу об уменьшении времени (сроков) выполнения проекта. При этом стоимость проекта увеличится, и можем найти зависимость стоимости проекта  от времени
от времени 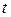 выполнения проекта как функцию вида
выполнения проекта как функцию вида  .
.
Пусть сетевой график имеет вид:
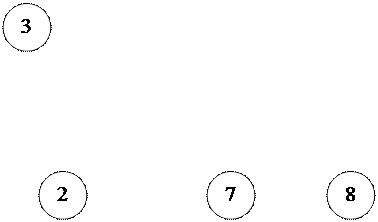
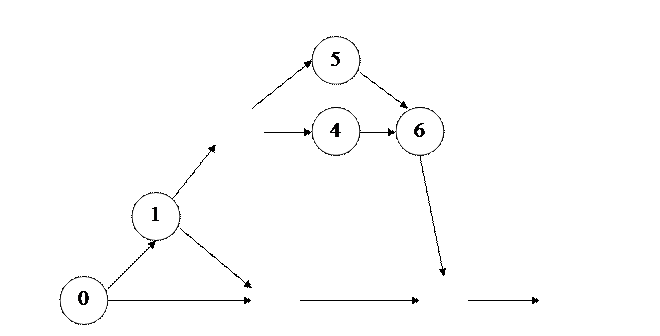
Рис.13.
Исходные данные для оптимизации представлены в таблице 4.
Таблица 4.
|
№ n/n
|
Работа
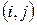
| Продолжительность работы
| Коэффициенты затрат на ускорение работы 
| Стоимость работы
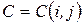
|
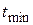
|
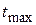
|
|
| (0,1)
|
|
|
|
|
|
| (0,2)
|
|
|
|
|
|
| (1,2)
|
|
|
|
|
|
| (1,3)
|
|
|
|
|
|
| (2,7)
|
|
|
|
|
|
| (3,4)
|
|
|
|
|
|
| (3,5)
|
|
|
|
|
|
| (4,6)
|
|
|
|
|
|
| (5,6)
|
|
|
|
|
|
| (6,7)
|
|
|
|
|
|
| (7,8)
|
|
|
|
|
Предположим, что стоимость работы 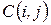 соответствует
соответствует  и первоначальная продолжительность работы
и первоначальная продолжительность работы  . Решим задачу об уменьшении сроков выполнения проекта за счет увеличения стоимости с начальных
. Решим задачу об уменьшении сроков выполнения проекта за счет увеличения стоимости с начальных 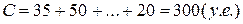
Для этого найдем все полные пути сетевого графика. Их оказывается четыре:
 , с
, с 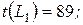
 , с
, с 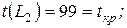
 , с
, с 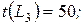
 , с
, с 
Представим эти пути графически в виде цепочек, где над стрелками отметим  , а под стрелками -
, а под стрелками - 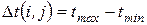 - это время, на которое можно уменьшить продолжительность работы.
- это время, на которое можно уменьшить продолжительность работы.
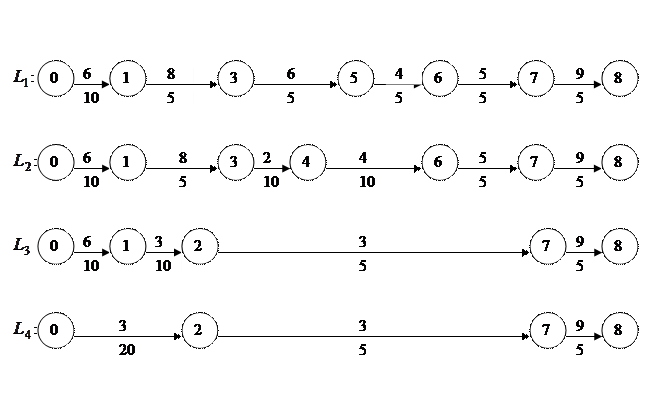
Рис. 14.
1-ый шаг. Уменьшаем длину критического пути 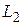 за счет работы (3,4), имеющей наименьший коэффициент затрат на ускорение. Тогда
за счет работы (3,4), имеющей наименьший коэффициент затрат на ускорение. Тогда  а стоимость проекта увеличится на
а стоимость проекта увеличится на 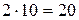 (у.е.), то есть до 320 у.е. На отрезке
(у.е.), то есть до 320 у.е. На отрезке 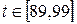 стоимость будет меняться как
стоимость будет меняться как
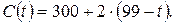
2-ой шаг. Имеем два критических пути  и
и 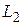 . Сократим их длины одновременно. Для этого используем работу (6,7) с наименьшим
. Сократим их длины одновременно. Для этого используем работу (6,7) с наименьшим 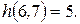 Тогда продолжительность проекта уменьшится на 5 дней, то есть
Тогда продолжительность проекта уменьшится на 5 дней, то есть  а стоимость увеличится на
а стоимость увеличится на  у.е. до 320+25=345 у.е. А на отрезке
у.е. до 320+25=345 у.е. А на отрезке  :
:
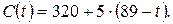
3-ий шаг. Берем работу (0,1) с 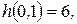 и
и  Тогда
Тогда 
 и на отрезке
и на отрезке 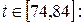
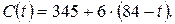
4ы-й шаг. Берем работу (1,3) с 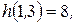
 Тогда
Тогда 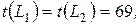
 и
и
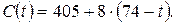
5ы-й шаг. Берем работу (7,8) с 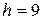 и
и  Тогда
Тогда 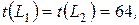
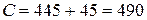 и
и
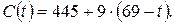
6-ой шаг. Теперь на  остались работы (3,5) и (5,6), а на
остались работы (3,5) и (5,6), а на 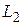 работа (4,6). С учетом наименьшего
работа (4,6). С учетом наименьшего  сократим на 5 дней выполнения работы (5,6) и (4,6).
сократим на 5 дней выполнения работы (5,6) и (4,6).
Получим 
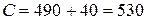 и
и
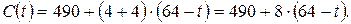
7-ой шаг. Остались: на  работа (3,5), а на
работа (3,5), а на 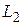 работа (4,6) со стоимостью затрат 6+4=10. Тогда
работа (4,6) со стоимостью затрат 6+4=10. Тогда 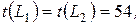
 и
и
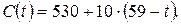
Таким образом продолжительность проекта удалось сократить до 54 дней за счет увеличения стоимости проекта до 580 у.е.
График зависимости стоимости 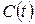 от продолжительности
от продолжительности 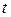 проекта будет представлять собой кусочко-линейную функцию.
проекта будет представлять собой кусочко-линейную функцию.

Рис.15.
С помощью этого графика можно, во-первых, оценить минимальную стоимость проекта при любом сроке выполнения 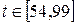 ; во-вторых, найти предельную продолжительность проекта при любой заданной стоимости
; во-вторых, найти предельную продолжительность проекта при любой заданной стоимости  .
.
Можно было решить эту задачу и в обратном порядке, взяв  и
и 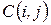 как стоимость
как стоимость 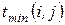 . Тогда речь пойдет о снижении стоимости проекта за счет увеличения продолжительности работ сначала на некритических путях (с
. Тогда речь пойдет о снижении стоимости проекта за счет увеличения продолжительности работ сначала на некритических путях (с 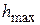 ), а потом и на критических путях.
), а потом и на критических путях.

 от времени
от времени 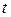 выполнения проекта как функцию вида
выполнения проекта как функцию вида  .
.

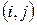

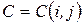
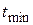
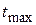
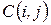 соответствует
соответствует  и первоначальная продолжительность работы
и первоначальная продолжительность работы  . Решим задачу об уменьшении сроков выполнения проекта за счет увеличения стоимости с начальных
. Решим задачу об уменьшении сроков выполнения проекта за счет увеличения стоимости с начальных 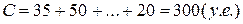
 , с
, с 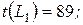
 , с
, с 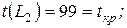
 , с
, с 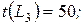
 , с
, с 
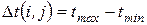 - это время, на которое можно уменьшить продолжительность работы.
- это время, на которое можно уменьшить продолжительность работы.
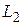 за счет работы (3,4), имеющей наименьший коэффициент затрат на ускорение. Тогда
за счет работы (3,4), имеющей наименьший коэффициент затрат на ускорение. Тогда  а стоимость проекта увеличится на
а стоимость проекта увеличится на 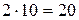 (у.е.), то есть до 320 у.е. На отрезке
(у.е.), то есть до 320 у.е. На отрезке 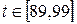 стоимость будет меняться как
стоимость будет меняться как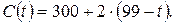
 и
и 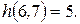 Тогда продолжительность проекта уменьшится на 5 дней, то есть
Тогда продолжительность проекта уменьшится на 5 дней, то есть  а стоимость увеличится на
а стоимость увеличится на  у.е. до 320+25=345 у.е. А на отрезке
у.е. до 320+25=345 у.е. А на отрезке  :
: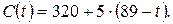
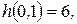 и
и  Тогда
Тогда 
 и на отрезке
и на отрезке 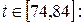
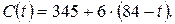
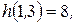
 Тогда
Тогда 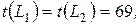
 и
и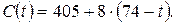
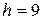 и
и 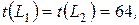
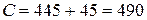 и
и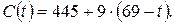
 сократим на 5 дней выполнения работы (5,6) и (4,6).
сократим на 5 дней выполнения работы (5,6) и (4,6).
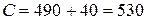 и
и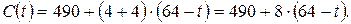
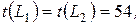
 и
и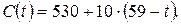
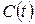 от продолжительности
от продолжительности 
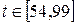 ; во-вторых, найти предельную продолжительность проекта при любой заданной стоимости
; во-вторых, найти предельную продолжительность проекта при любой заданной стоимости  .
. и
и 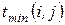 . Тогда речь пойдет о снижении стоимости проекта за счет увеличения продолжительности работ сначала на некритических путях (с
. Тогда речь пойдет о снижении стоимости проекта за счет увеличения продолжительности работ сначала на некритических путях (с 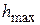 ), а потом и на критических путях.
), а потом и на критических путях.


