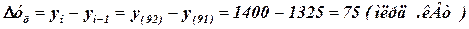Абсолютные и относительные показатели рядов динамики.
Динамический ряд представляет собой ряд последовательных уровней, сопоставляя которые между собой можно получить характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики, к числу которых относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Если сравнению подлежат несколько последовательных уровней, то возможны следующие два варианта сопоставления: 1) каждый уровень ряда динамики сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения. В качестве базисного уровня (базы сравнения) выбирается либо начальный уровень ряда динамики или же уровень, с которого начинается какой-то новый этап развития явления. Такое сравнение называется сравнением с постоянной базой; 2) каждый уровень ряда динамики сравнивается с непосредственно ему предшествующим. Такое сравнение называется сравнением с переменной базой. Показатели динамики с постоянной базой – базисные показатели – характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i -гo) периода. Показатели динамики с переменной базой – цепные показатели – характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени. Абсолютный прирост базисный абсолютный прирост: цепной абсолютный прирост: где
Темп роста базисный коэффициент роста: цепной коэффициент роста: базисный темп роста: цепной темп роста: Темп прироста базисный темп прироста: цепной темп прироста: При анализе относительных показателей ряда динамики (темпов роста и темпов прироста) не следует рассматривать их изолированно от абсолютных показателей (уровней ряда и абсолютных приростов) Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением одного процента прироста. Этот показатель рассчитывают как отношение абсолютного прироста к темпу прироста (в процентах) за тот же период времени:
Рассмотрим расчет вышеуказанных показателей по ряду динамики производства электроэнергии, представленному в табл. 11.4. Таблица 11.4 Производство электроэнергии
1. Определим абсолютный прирост. Базисный: Абсолютный прирост производства электроэнергии в 1992 г по сравнению с 1990 г составил 100 млрд. кВт. Цепной: Абсолютный прирост производства электроэнергии в 1992 г по сравнению с 1991 г составил 75 млрд. кВт. Результаты расчета приведены в табл. 11.4.
2. Определим темп роста производства электроэнергии:
Производство электроэнергии в 1992 году по сравнению с 1990г. возросло до 107,9 %. Результаты расчета приведены в табл. 22.
3. Определим темп прироста производства электроэнергии:
100 млрд. кВт электроэнергии произведенной в 1992 году дали 7,9% прироста.
4. Определим абсолютное значение одного процента прироста производства электроэнергии:
Абсолютное значение одного процента прироста в 1992 г. составило 13,25 млрд. кВт электроэнергии.
|

 определяется как разность между двумя уровнями ряда динамики и показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:
определяется как разность между двумя уровнями ряда динамики и показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения: (11.1)
(11.1)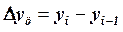 (11.2)
(11.2)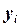 – уровень сравниваемого периода;
– уровень сравниваемого периода; – уровень базисного периода;
– уровень базисного периода; – уровень непосредственно предшествующего периода.
– уровень непосредственно предшествующего периода. определяется как отношение двух сравниваемых уровней, может быть выражен с помощью коэффициентов (коэффициент роста
определяется как отношение двух сравниваемых уровней, может быть выражен с помощью коэффициентов (коэффициент роста 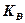 ) или в процентах, и показывает, во сколько раз данный уровень превышает уровень базисного периода:
) или в процентах, и показывает, во сколько раз данный уровень превышает уровень базисного периода: ; (11.3)
; (11.3) ; (11.4)
; (11.4) ; (11.5)
; (11.5) . (11.6)
. (11.6) показывает на сколько процентов уровень данного периода больше (или меньше) базисного уровня:
показывает на сколько процентов уровень данного периода больше (или меньше) базисного уровня: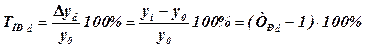 (11.7)
(11.7)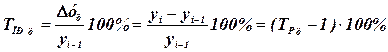 (11.8)
(11.8)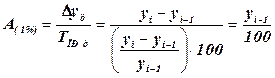 (11.9)
(11.9)