Алгоритм применения ранговой корреляции Спирмена для оценки степени связи признаков.
Проранжировать значения первой переменной, начисляя ранг 1 наименьшему значению, и записать ранги в первый столбец по порядку номеров испытуемых или по возрастанию ранга, при равных переменных им присваивается одинаковый среднеарифметический ранг. Проранжировать значения второй переменной по тем же правилам и занести соответствующие ранги во второй столбец. Подсчитать разности Квадраты При наличии одинаковых рангов рассчитать поправки:
где
Рассчитать коэффициент ранговой корреляции Спирмена по формуле:
а)
б) при наличии одинаковых рангов
где - количество испытуемых, участвовавших в ранжировании.
7. Определить по таблице критические значения для данного. Если, то корреляция достоверно отличается от 0 (этот пункт будет рассмотрен в следующем параграфе). Пример 178. Найти коэффициент ранговой корреляции Спирмена по связи эмоционального состояния и зрительной памяти после иппотерапии по результатам исследования.
при
Связь между двумя качественными признаками можно оценить, используя выборочный коэффициент ранговой корреляции Кендалла:
и
Пример 179. Определите степень связи итогов чемпионата России по футболу в премьер-лиге и результаты первого круга 2002 года.
Решение. Определим степень связи по выборочному коэффициенту ранговой корреляции Кендалла.
и между итогом чемпионата и результатом первого круга существует прямая средней тесноты связь.
Если статистическая информация о многомерном признаке представлена в порядковой шкале, то измерение парных связей осуществляется через коэффициенты ранговой корреляции Кендалла или Спирмена.
Пример 180. Три арбитра оценили мастерство 10 фигуристов, в итоге были получены три последовательности рангов:
Найдите матрицу ранговой корреляции Спирмена и пару арбитров, оценки которых наиболее согласуются. Решение. Найдем
и
Поскольку коэффициент
|

 между рангами и по каждой строке и занести их в третий столбец.
между рангами и по каждой строке и занести их в третий столбец.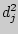 занести в четвертый столбец и подсчитать их сумму
занести в четвертый столбец и подсчитать их сумму 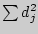 .
.
 - объем каждой группы одинаковых рангов в ранговых рядах и.
- объем каждой группы одинаковых рангов в ранговых рядах и. , при отсутствии одинаковых рангов;
, при отсутствии одинаковых рангов;

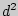
 620
620
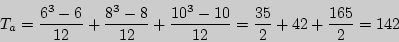
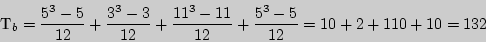



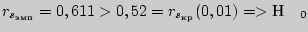 - отвергается.
- отвергается.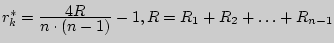
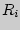 - число рангов
- число рангов  ,...,
,...,  , больших
, больших 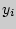 .
. = 9,
= 9, 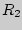 = 8,
= 8,  = 7,
= 7, 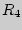 = 0,
= 0, 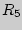 = 3,
= 3,  = 4,
= 4, 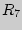 = 1,
= 1,  = 1,
= 1, 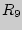 = 1, тогда
= 1, тогда  ,
,  , a
, a 
 , вычислив сумму квадратов разностей
, вычислив сумму квадратов разностей  рангов арбитров А и В.
рангов арбитров А и В.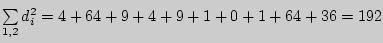
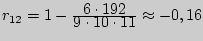 аналогично находим, что
аналогично находим, что 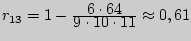 и
и 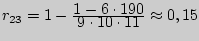 , а искомая матрица ранговой корреляции Спирмена выглядит следующим образом
, а искомая матрица ранговой корреляции Спирмена выглядит следующим образом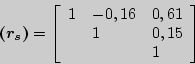
 является максимальным, то оценки арбитров А и С наиболее согласуются.
является максимальным, то оценки арбитров А и С наиболее согласуются.


