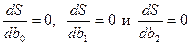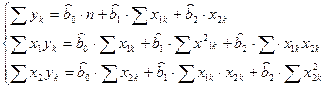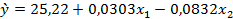ОЦЕНКА КОЭФФИЦИЕНТОВ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
В качестве оценок параметров
Значения
В результате получим систему линейных уравнений:
Подставим известные значения и получим следующую систему линейных уравнений:
Решаем систему, применяя инструмент ППП EXCEL – Поиск решения. Полученные результаты представлены в таблице 5. Таблица 5 – Результат вычислений с помощью функции Поиск решений - ППП EXCEL
Таким образом, получаем уравнение множественной регрессии:
Значение коэффициентов при объясняющих переменных очень мало, что указывает на очень малое влияние объясняющих переменных на результативный фактор, поэтому факторы x1 и x2, силу влияния которых оценивает b1 и b2, можно считать несущественно влияющими, неинформативными.
|
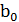и 
принимаются величины 
и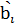 
, минимизирующие сумму квадратов отклонений наблюдаемых значений результативного признака 
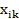от расчётных теоретических значений.
и 
и 
