РАСЧЁТ ОБЩЕГО И ЧАСТНОГО F-КРИТЕРИЯ ФИШЕРА.
Общий F-критерий проверяет гипотезу H0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2=0)
где n – число наблюдений, m – количество факторов Получаем следующий результат Fнабл= 0,9025 По таблицам распределения находим критическое значение F-критерия в зависимости от уровня значимости α (обычно его берут равным 0,05) и двух чисел степеней свободы k1=m-1=3 – 1 =2; k2= n-m =21- 3=18, где m –количество факторов, а n – число наблюдений. Получаем F табл = 3,55. Так как Fтабл > Fфакт, то с вероятностью 0,95 делаем заключение о статистической незначимости уравнения в целом и показателя тесноты связи, которые сформировались под почти случайным воздействием факторов x1 и x2. Частные F-критерии Fх1 и Fх2 оценивают статистическую значимость присутствия факторов x1 и x2 в уравнении множественной регрессии, Fх1 оценивают целесообразность включения в уравнение фактора x1 после того, как в него был включен фактор x2. Соответственно, Fх2 указывает на целесообразность включения в уравнение фактора x2 после того, как в него был включен фактор x1.
После расчётов в ППП EXCEL получаем F табл > F x1факт, приходим к выводу о не целесообразности включения в модель фактора x1 Рассчитываем
После расчётов в ППП EXCEL получаем Низкое значение
|
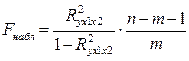
= 0,902. Сравниваем с Fтабл = 3,55. Видим, что
= 0,806
за счёт включения в модель фактора x2 после фактора x1. Низкое значение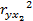 
за счёт включения в модель фактора x1 после фактора x2.
