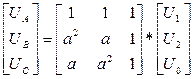Метод симметричных составляющих. При несимметричных повреждениях в трехфазной системе нельзя рассматривать процесс только в одной фазе
При несимметричных повреждениях в трехфазной системе нельзя рассматривать процесс только в одной фазе, поскольку явления, происходящие в разных фазах, различны. Для расчетов несимметричных режимов применяется метод симметричных составляющих. Суть метода заключается в том, что любую несимметричную систему трех векторов всегда можно разложить (рис. 1.7) на три симметричные системы (последовательности): - прямую, - обратную, - нулевую. Система прямой последовательности состоит из трех равных векторов А 1, В 1, С 1, сдвинутых по фазе на угол 120° с прямым порядком чередования фаз А 1, В 1, С 1. Система обратной последовательности состоит также из трех равных векторов А 2, В 2, С2, сдвинутых по фазе на угол 120°, но с обратным порядком чередования фаз А 2, С 2, В 2. Система нулевой последовательности состоит из трех одинаковых векторов А 0, В 0, С 0, совпадающих по направлению друг с другом.
а) б) в) г)
Рис. 1.7. Несимметричная трехфазная система векторов А, В, С (а) и ее представление системами прямой А 1, В 1, С 1 (б), обратной А 2, С 2, В 2 (в) и нулевой А 0, В 0, С 0 (г) последовательностями
Связь между векторами А, В, С несимметричной системы и векторами А 1, А 2, А 0 симметричных систем определяется матричным соотношением
где а = – 1/2+j√3/2=е-j120 – оператор поворота вектора на 120° против часовой стрелки. При умножении вектора на оператор а вектор поворачивается на 120° против часовой стрелки, при умножении вектора на а 2 вектор поворачивается на 240° против часовой стрелки. В частности, вектор В несимметричной системы есть сумма вектора А 1 прямой последовательности, повернутого на 240° против часовой стрелки, вектора А 2 обратной последовательности, повернутого на 120° против часовой стрелки, и вектора А 0 нулевой последовательности: В = а 2× А 1+ а×А 2+1× А 0. Связь между векторами А 1, А 2, А 0 симметричных систем и векторами А, В, С несимметричной системы определяется матричным соотношением
В частности, вектор А 1 прямой последовательности есть одна треть от суммы вектора А несимметричной системы, вектора В несимметричной системы, повернутого на 120° против часовой стрелки, и вектора С несимметричной системы, повернутого на 240° против часовой стрелки, А 1= Применительно к токам и напряжениям в точке несимметричного КЗ можно записать:
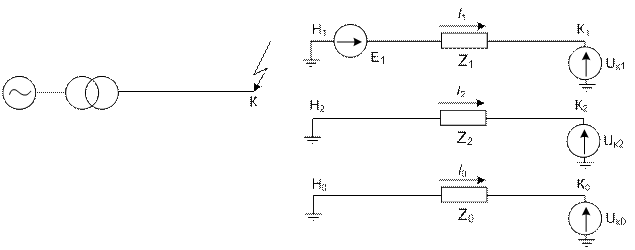
или I A= I 1+ I 2+ I 0; U A= U 1+ U 2+ U 0; I В= а 2 I 1+ аI 2+ I 0; U В= а 2 U 1+ аU 2+ U 0; (1.5) I С= аI 1+ а 2 I 2+ I 0; U С= аU 1+ а 2 U 2+ U 0. Метод симметричных составляющих для расчета несимметричных режимов основывается на следующих положениях: - несимметричная трехфазная схема (рис. 1.8, а) рассматривается в виде трех отдельных схем (рис. 1.8, б), соответствующих трем симметричным системам: прямой, обратной и нулевой последовательностей; - элементы, входящие в исходную электрическую схему, представляются в указанных трех схемах соответствующими сопротивлениями прямой Z 1,обратной Z 2 и нулевой Z 0последовательностей;при этом следует учитывать отличие сопротивлений Z 1, Z 2, Z 0 отдельных элементов схемы; - источники ЭДС имеются только в схеме прямой последовательности; - в каждой схеме протекает ток соответствующей последовательности; - напряжения трех последовательностей U 1, U 2, U 0 считаются приложенными (возникающими) в месте повреждения рассматриваемой цепи. На схемах рис. 1.8, б обозначены: Е 1 – эквивалентная ЭДС прямой последовательности; I 1, I 2, I 0 – токи прямой, обратной и нулевой последовательностей; U 1, U 2, U 0 – напряжения прямой, обратной и нулевой последовательностей; Н и К – начало и конец схемы.
а) б)
Рис.1.8. Принципиальная схема с несимметричным повреждением в точке К (а) и схемы прямой, обратной и нулевой последовательностей (б)
Расчет токов I 1, I 2, I 0 и напряжений U 1, U 2, U 0 каждой последовательности ведется в соответствии с законами теоретической электротехники. Результирующие токи и напряжения в точке несимметричного КЗ рассчитываются по выражениям (1.5).
|


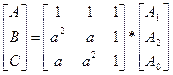 , (1.4)
, (1.4) .
. (А + а 2 ×В + а × С).
(А + а 2 ×В + а × С). ;
;