Заломлення променя сферичною поверхнею. Сферичне дзеркало.
Нехай сферична поверхня радіусу r з центром в точці С розділяє два середовища з показниками заломлення n і n’ (рис. 6.1). Оптична вісь перехрещується з поверхнею в точці О, що називається вершиною поверхні. Промінь, що виходить із точки S заломлюється на поверхні в точці М і перехрещується з оптичною віссю в точці S’. позначимо положення точок S і S’; згідно правилу знаків, відрізками – а і а’, а кути між променями і оптичною віссю – и і и’. Для параксіальних променів дугу ОМ можна замінити прямолінійним відрізком КМ=h, а закон заломлення записати виразом
Рис.6.1. Хід променів у сферичному дзеркалі CM=r Із D МС і DМС, враховуючи правило знаків, справедливо записати, що
Підставляючи (2.16) і (2.17) в (2.15), отримаємо
Враховуючи малість кутів, можна записати
З урахуванням (2.19) вираз (2.18) має вигляд
або
Формула (2.20) називається нульовим інваріантом Аббе. Із неї можна отримати фокусну відстань однієї сферичної поверхні. Так, для променів, що йдуть із простору предметів паралельно оптичній вісі, тобто а=¥ і а’=f’, із (2.20), отримаємо
Звідки задня фокусна відстань
якщо ж а’=¥, то а=f і тоді із формули (2.20) передня фокусна відстань заломлюючої поверхні
Відношення фокусних відстаней дає
тобто відношення фокусних відстаней заломлюючої поверхні відповідно пропорційні показником заломлення середовищ, що розділяються нею. Інваріант Аббе перетворений до вигляду
називається основним рівнянням заломлюючої поверхні. Якщо в рівнянні (2.24) замінити n’ на -n, тобто застосувати поверхню для відбиття, то отримаємо формулу сферичного дзеркала, виражену через радіус.
Фокусну відстань сферичного дзеркала можна знайти:
таким чином, формулу сферичного дзеркала (2.25), з урахуванням (2.26), можна записати у вигляді
Для плоского дзеркала, припускаючи r=¥, із (2.25) отримаємо:
Призми Призмою називається оптична деталь, що обмежена заломлюючими і відбиваючими плоскими поверхнями, розташованими під кутом одна до одної. В геодезичних приладах застосовуються призми двох видів: відбивні і заломлюючі. Відбивні призми призначаються для зміни напряму світлового пучка шляхом відбиття його від граней призми. При цьому використовується або явище повного внутрішнього відбиття або просте відбиття. Для підсилення ефекту відбиття відбивні грані інколи сріблять. Відбивні призми застосовуються в геодезичних приладах з ціллю: − зміни напряму оптичної вісі приладу (призма в ломаній трубі астрономічного універсалу); − зміни напряму лінії візування і лінії спостереження (окулярні призми відповідно зорової труби і оптичного мікрометра); − обернене зображення; − розділення зображення.
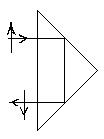
Рис.7.1. Призма АР-90º Рис.7.2. Призма БР-180º Рис.7.3. Призма БС-0º Відбивні призми, по суті, виконують ту ж роль, що і плоскі дзеркала, але мають перед ними ряд переваг: їх легше закріпити, вони зберігають незмінними взаємне положення відбивних поверхонь, забезпечують менші втрати світла. Відбивні призми позначаються двома буквами і числом градусів в куті, на який відхиляються промені після проходження через призму. Перша буква вказує кількість відбивних граней: А - одну, Б – дві, В – три. Друга буква характеризує геометрію призми: Р – рівнобедрена, С – ромбічна, П – пентапризма. Якщо одну із відбивних граней призми замінюють двома, розташованими під кутом 90°, роблячи над нею надбудову у вигляді даху (для зміни не зовсім оберненого зображення на цілком обернене або навпаки), то такі призми називаються призмами з дахом і позначення добавляється маленька буква “д”, наприклад, “Ад”. Відбивні призми, як плоско-паралельні пластинки, перекручують похилі пучки променів, що сходяться. Тому призми намагаються розташовувати в паралельних або близьких до паралельних променях. Видів відбивних призм багато. Розглянемо такі, що найбільше застосовуються в геодезичних приладах. Прямокутна призма АР=90° (рис. 7.1) з однією відбивною гранню. В головному її є рівнобедрений прямокутний трикутник. Призма змінює напрям променів на 90° і дає дзеркальне зображення. Кожна відбивна призма характеризується коефіцієнтом призми. Коефіцієнтом призми називається відношення ходу променів в призмі d=АВ+ВС до діаметра отвору вхідної грані D=LМА:
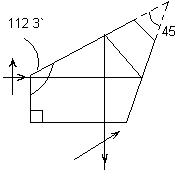
для призми АР=90°, К=1 Прямокутна призма БР=180° (рис. 7.2) з двома відбивними гранями. Призма змінює напрям променів на 180° і зберігає вид зображення. Призма володіє важливою особливістю: при обертанні призми навкруги ребра, що знаходяться горизонтально, зображення не зміщується. Ця перевага дала можливість широкого застосування призми БР=180° при роботі з автоколіматорами і автоколімаційними теодолітами. При нахилі ребра призми в вертикальній площині на кут a і розвороті призми навкруги ребра на кут b, вихідний світловий промінь змінить напрям азимутальній площині на величину Dg, що визначається за формулою [17].
Значення кутів a і b визначається відповідно горизонтальністю положення ребра і вертикальністю вхідної грані призми. Коефіцієнт призми БР=180°, К=2. Призма-ромб БС=0° (рис. 7.3) призначається для зміщення оптичної вісі без зміни орієнтації зображення. Вона має дві паралельні заломлюючі і дві паралельні відбивні грані. Призма БС=0° має застосування, наприклад в точних теодолітах для почергового спостереження горизонтального і вертикального лімбів.
Рис.7.4. Призма Дове АР-0° Рис7.5. Пентапризма БП-90° Призму Дове АР=0° (рис. 7.4) легко отримати із прямокутної призми АР=90°; якщо зрізати верхню неробочу її частину. Призма Дове обертає зображення зверху вниз, зберігаючи напрям ходу променів. При повороті призми в площині відбивної грані на кут a, зображення обертається на кут 2a. Пентапризма БП=90° (рис. 7.5) призначається для зміни напряму ходу променів на 90°. Вона має дві заломлюючі грані, розташовані взаємно під кутом 90°, і дві відбивні грані розташовані під кутом 45°. Між відбивною і суміжною заломлюючою гранями – кут 112,5°, коефіцієнт призми БП=90° К=3,4142 Часто замість БП-90° виготовляють оптичну деталь з таким же функціональним призначенням але значно меншої ваги і габаритів – пентаблок. Пентаблок (рис. 7.5) має два плоскі дзеркала, наклеєні торцями вертикально на загальну основу під кутом 45° між відбивними поверхнями. Атестація кута відхилення променів пентаблоком (чи пентопризмою) виконується коліматорним чи автоколіматорним методами з середньою квадратичною похибкою 0,4².[10] Пентаблок широко використовується в спеціальних геодезичних приладах. При похилах пентаблоку чи пентапризми навкруги вихідного променя на кут a і вхідного променя на кут b вихідний світлий промінь буде змінювати свій напрям. Відхилення вихідного променя від положення коли пентаблок (чи пентапризма) знаходиться в горизонті, в азимутальній площині визначається за формулою
а в вертикальній площині за формулою
при нахилах a=b=2¢, похибка в азимутальний напрям відхилення Dgпьг=0,14². Призма – куб (рис. 7.6) призначається для відбиття і одночасно пропускання світлових променів у взаємно перпендикулярних напрямках. Вона складається із двох прямокутних призм склеєних із діагональними гранями. Діагональна грань однієї із призм покривається по всій площі частково відбитим шаром. Звично таким покриттям служить зовсім тонкий шар алюмінію або срібла. Для виключення повного внутрішнього відбиття променів діагональні грані склеюються піхтовим бальзамом, який володіє великою прозорістю і коефіцієнтом заломлення n=1,53, близьким до коефіцієнтів заломлення скла. В залежності від коефіцієнтів відбиття і пропускання діагонального шару змінюється яскравість зображення. Для виключення не збігання осей z’1 і z’2 необхідно щоб один із штрихів, що поступає на призму по відношенню до другого був дзеркальним.
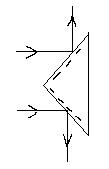
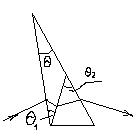
Рис7.6. Призма-куб К-О Рис.7.7. Світлороздільна призма Склеєна грань посріблена Призма – куб використовується для одночасного розповсюдження основного пучка променів по двох напрямках – безпосередньо по лінії візування і наприклад, через вимірювальні шкали, розташовані в стороні від лінії відбивання. Після сполучення променів в полі зору спостерігача раніше розділені пучки променів дозволяють бачити одночасно об’єкт спостереження і необхідну при ньому шкалу. Призма – куб має практичне застосування в автоколімаційних зорових трубах. Якщо дзеркальне покриття граней прямокутної рівнобедреної призми (рис. 7.7) буде зовнішнім, то падаючий паралельний пучок променів відіб’ється від обох дзеркальних граней, розділиться на дві частини і буде розповсюджуватись в протилежних напрямах. Така призма називається світло роздільною. Вона має застосування, наприклад в фотоелектричних автоколіматорах. Заломлюючі призми змінюють напрям променів світла шляхом заломлення їх при проходженні через призму. Грані призми, через які проходять промені світла при заломлені, називаються заломлюючими а створений заломлюючими гранями двогранний кут – заломлюючим кутом призми. Перетин А призми площиною перпендикулярною заломлюючому ребру називають головним перетином призми. В геодезичних приладах використовуються заломлюючі призми з кутом між заломлюючими гранями ≤5°. Такі призми називаються оптичними клинами. Знайдемо для кута e (рис. 7.8), на який відхиляється від свого первісного напряму промінь, що пройшов через призму, виразивши через постійні величини: показник заломлення призми n її заломлюючий кут q і показник заломлення no середовища, в якому розташована призма. Згідно закону відбиття світла, для малих кутів падіння, із DN1MN2 можна записати
У відповідності з законом заломлення маємо
Для призм, розташованих у повітрі показник заломлення =1. Для малих кутів із виразу у (2.33) отримаємо:
З урахуванням значень кутів із (2.35) вираз (2.33) запишемо у вигляді:
Враховуючи із DN1KN2
Із формули (2.37) видно, що для оптичного клина при малих кутах падіння відхилення e не залежить від кута падіння променя і1. Це дає можливість використовувати оптичні клини для відхилення променя на постійний кут, наприклад, в далекомірах.
Рис.7.8. Оптичний клин Рис.7.9. Ахроматичний клин
Так як кут відхилення променів залежить від показника заломлення призми, то білий промінь, прийшовши через призму, буде зазнавати дисперсію – розкладатися на складові кольору. Для збереження різкості зображення предметів, що розглядаються через призми або клини, застосовують ахроматичні призми і клини. Ахроматичний клин (рис. 7.9) складається, як правило, із двох клинів, виготовлених із різних сортів скла з відповідно підібраними показниками заломлення. За звичаєм один клин виготовляють із крону, а другий – із флінту. Склеюють клини так, щоб заломлюючі кути q¢ і q² були обернені в протилежні боки. Ахроматичний клин відхиляє промінь до основи на кут e, не розкладаючи його на складові частини спектру. 8. Лінзи Лінза – прозора деталь, обмежена двома сферичними заломлюючими поверхнями або однією плоскою і однією сферичною поверхнями. Лінза є найбільш поширена оптична деталь. До позитивних (збиральних) лінз (рис. 2.4. лекція №2) відносяться: двовипукла, плоска випукла і вгнуто - випукла, або меніск позитивний (товщина в центрі більша чим по краях). До негативних (розсіюючи) лінз (рис. 2.5. лекція №2) відносяться: двовгнута, плоско-вгнута і випукло – вгнута або меніск негативний (товщина в центрі менша чим по краях). Назви збиральних лінз закінчуються словом “випукла”, а розсіюючи – словом “вгнута” [15]. Інколи назва плоскавипуклої і плоско-вгнутої лінз можуть бути як випукло-плоска і вгнуто-плоска, в залежності від того якою є перша поверхня (плоскою чи сферичною). На рисунку r1 і r2– радіуси кривизни поверхонь лінзи. Як видно із рисунка збиральні лінзи товстіші на середній, а розсіюючі – по краях. Пряма с1с2, що з’єднує центри сферичних поверхонь лінз чи перпендикуляр опущений із центру сферичної поверхні на плоску поверхню називається оптичною віссю лінзи. Лінза збирає падаючий паралельний пучок променів в одну точку. Цю точку, що лежить на оптичній вісі називають фокусом лінзи. В просторі зображень, яка сполучена з нескінчено віддаленою точкою, що розташована на оптичній вісі в просторі предметів. Передній фокус – це точка на оптичній вісі в просторі предметів, яка сполучена з нескінчене віддаленою точкою, що розташована на оптичній вісі в просторі зображень. Задній і передній фокуси інколи називають фокусами простору предметів простору зображень [1]. Відстань від переднього фокусу до заломлюючої поверхні називається передньою фокусною відстанню лінзи (f). Аналогічно визначається задня фокусна відстань (f’). Слід зауважити, що лінза має дві заломлюючі поверхні і стає неочевидним від якої із них визначати фокусну відстань. Якщо лінза мала по відношенню до радіусів кривини заломлюючих поверхонь лінзи, то її називають тонкою. Головні площини в нескінчено тонкій лінзі практично збігаються і перетворюють в “середню” її площини. Цю “середню” площину називають головною площиною. В геодезичних приладах звично використовують не окремі лінзи, а їх системи, що складаються із двох і більше тонких лінз. Визначаючи фокусні відстані від середини поверхні лінзи, ми по суті, відраховуємо їх від головної площини, яка у випадку сферичної поверхні утворилась від злиття двох головних площин і проходить через вершину поверхні. Значення
де: n- показник заломлення; r1 і r2- радіуси кривини сферичних поверхонь (випукла “+”, вгнута “-“, плоска “¥”). Для товстої лінзи
де d– товщина лінзи. 9. Центрована і ідеальна оптичні системи. Кардинальні площини і точки. Збільшення оптичної системи Реальні оптичні системи мають по меншій мірі дві заломлюючі поверхні (лінза), а частіше мають комбінацію лінз. В геодезичних приладах особливо важливу роль займають центровані оптичні системи з сферичними заломлюючими і відбивними поверхнями. Систему із декількох заломлюючих поверхонь називають центрованою оптичною системою, якщо центри поверхонь оптичних деталей розташовані на одній прямій, що називається головною оптичною віссю системи. Оптична вісь системи – це пряма, що проходить через оптичну вісь системи, її називають меридіональною. Таким чином, оптична вісь центрованої системи – лінія перехрещення всіх меридіональних площин. Гаус створив теорію ідеальної оптичної системи, тобто системи, в якій зберігається гомоцентричність пучків і зображення геометрично подібні предмету. В ідеальній системі кожній точці, лінії і площині простору предметів відповідає сполучена їй точка, лінія або площина в просторі зображень, тобто зображення відповідає предмету без перекручень. Ідеальна оптична система може бути здійснена, якщо в центрованій оптичній системі обмежитись параксіальною областю [18]. Теорія Гауса встановлює для ідеальної оптичної системи декілька так званих кардинальних (головних) площин і відповідних їм кардинальних точок. Якщо кардинальні площини і точки задані ми можемо користуватись оптичною системою, не розглядаючи реального ходу променів в ній. Для ознайомлення з ними оптичну систему зручно представити у вигляді двох сфер заломлення поверхонь (рис. 2.12, лекція №2) з вершинами у точках О і О’ – точки перехрещення сферичних заломлюючих поверхонь з оптичною віссю. Точка в якій перехрещуються заломлені промені паралельні оптичні осі називається фокусом: F- передній фокус, для променів, що йдуть із простору зображень; F’- задній фокус, для променів, що йдуть із простору предметів. Площини, що проходять через передній і задній фокуси перпендикулярно до оптичної вісі називаються передньою і задньою фокальними площинами. Заломлюючу дію поверхонь оптичної системи можна звести до однієї площини: а) для променів, що йдуть із простору предметів, площинf називається задньою головною площиною; б) для променів, що йдуть із простору зображень, площина називається передньою головною площиною. Точки перехрещення N і N’ головних площин з оптичною віссю називається відповідно передньою і задньою головними точками. Головні точки і головні площини відіграють в системі роль початку відліку: − відстань f=NF від передньої головної точки до переднього фокусу називається передньою фокальною відстанню; − відстань f’=N’F’ від задньої головної точки до заднього фокусу називається задньою фокальною відстанню. Відстань SF=OF від вершини передньої поверхні до переднього фокусу називається переднім фокальним відрізком. Відстань S’F=O’F’ від вершини задньої поверхні до заднього фокусу називається заднім фокальним відрізком. Положення предмету і його зображення в центральній системі визначаються відрізками а і а, які (з урахуванням знаків) також відраховуються відповідно від передньої і задньої головних точок. Якщо в просторах предметів і зображень одне і те ж середовище (наприклад повітря) де n=n’, то згідно (2.23)
Формула (2.40) виражає оптичну (заломлюючу) силу системи. Чим більше оптична сила, тим ближче до оптичної системи розташовується зображення предмету, але тим менша величина цього зображення. За одиницю вимірювання оптичної сили системи приймається діоптрія (як і для лінзи), тобто оптична сила системи, що має фокусну відстань f’=1 м. Для побудови зображення в центровані системі використовуються три промені, хід яких такий (рис. 2.12, лекція №2): 1) промінь ВМ, що падає на систему паралельно оптичній вісі, після заломлення в системі проходить через задній фокус F’; 2) промінь ВF, що проходить через передній фокус, після заломлення в системі виходить паралельно оптичній вісі; 3) промінь ВN, що проходить через головну точку системи. Після заломлення виходить не змінюючи свого напряму. Всі падаючі промені проводять до передньої головної площини. Промені, що виходять із системи, перехрещуються з задньою головною площиною на тій же висоті. Відношення лінійного розміру зображення l’ до лінійного розміру предмету l називається лінійним збільшенням центрованої системи:
Візьмемо від точки А промінь на точку М, що проходить під кутом до оптичної вісі. Йому в просторі зображень буде відповідати промінь М’А’, що складає з оптичній віссю кут и’. Відношення:
називається кутовим збільшенням. Між лінійним і кутовим збільшенням існує заломлення:
Відношення (2.43) справедливо, якщо показники заломлення першої і останньої поверхонь системи є однаковим, наприклад, коли з обох боків системи є повітря. 10. Складання центрованих оптичних систем. Телескопічна система Звичайно окремі частини оптичних приладів (об’єктиви, окуляри) складаються із декількох лінз, які створюють центровану систему з загальною оптичною віссю. Складна центрована система складається, таким чином, із декількох простих систем – лінз, що мають заломлюючі поверхні і визначаються своїми головними площинами і фокусами. Таку складну систему із декількох лінз замінюють еквівалентною, визначивши для неї положення головних площин і фокусів. Еквівалентна система має на відміну від простої не одну, а дві головні площини: передню і задню. Відшукування головних площин і фокусів еквівалентної системи по заданих відповідних елементах простих систем називають складанням систем. Відрізок D оптичної вісі між заднім фокусом першої системи і переднім фокусом другої системи називають оптичним інтервалом∆(рис.2.12, лекція №2)
Представимо складну оптичну систему з двох сферичних поверхонь. Перша система задається положенням головних площин Н1 і Н’1, переднього і заднього фокусів, а друга – відповідно положення Н2 і Н’2, F2 F’2. Відстань між головною площиною першої і передньою головною площиною другої системи H’1H2=d. Промінь Р з простору променів, паралельний оптичній вісі, заломиться в точці М’1, пройде через задній фокус першої системи і заломиться другими головними площинами Н2 і Н’2 в точках N2 і N’2. Після перетину з оптичною віссю в точці F’, що називається заднім головним фокусом еквівалентної системи, промінь зустрічається з геометричним продвиженням свого вихідного напряму в точці М’. Перпендикуляр до оптичної вісі в точці М’ називається задньою головною площиною еквівалентної системи. Позначимо положення заднього головного фокуса другої системи величиною F’, а відносно задньої головної площини Н’– величиною f’e, що називається задньою фокальною відстанню еквівалентної системи. Аналогічно промінь Р з простору зображень, паралельний оптичній вісі, заломиться в точці М2, пройде через передній фокус F2 другої системи і заломиться головними площинами першої системи Н’1 і Н1 в точках N’1 i N1. Після перетину з оптичною віссю в точці F, що називається переднім головним фокусом еквівалентної системи, промінь зустрічається з геометричним продовженням свого вихідного напряму в точці М. Перпендикуляр до оптичної вісі в точці М називається передньою головною площиною еквівалентної системи. Позначимо положення переднього головного фокусу еквівалентної системи величиною cF, а відносно передньої головної площини Н – величиною fe, що називається передньою фокальною відстанню еквівалентної системи. Положення переднього і заднього фокусів еквівалентної оптичної системи, а також фокальні відстані визначаються за формулами (1.6).
Із рис. 2.18 видно, що
Підставимо в (2.49) і (2.50) відповідні значення із (2.45)
Формули (2.51) і (2.52) дозволяють визначити положення головних площин еквівалентної оптичної системи. Відстань між головними площинами еквівалентної оптичної системи визначається за формулою:
Еквівалентна оптична система може бути повністю охарактеризована чотирма по різному сполученими величинами:
або
або
Іншими словами, люба оптична система може бути представлена положеннями: оптичної вісі, передньої і задньої головних площин, а також переднього і заднього головних фокусів. Для геодезичних приладів особливо важливі телескопічні системи. Телескопічною або фокальною системою називають систему, в якій оптичний інтервал D=0, тобто задній фокус першої системи збігається з переднім фокусом другої. Фокальні відстані телескопічної системи згідно (2.47) і (2.48) дорівнюють
Таким чином до телескопічних систем відносять зорові труби, що сфокусовані на нескінченність для нормального ока. Це означає, що паралельний пучок променів після заломлення в оптичній системі залишається паралельним. Відповідно до (2.51) і (2.52) головні площини оптичної системи будуть також знаходитись в нескінченності
В телескопічних системах з паралельним пучком променів апертурною діафрагмою буде оправа об’єктива. Вона ж буде і вхідною зіницею (Dоб.). Зображення цієї діафрагми в просторі зображень буде вихідною зіницею (dок) оптичної системи. Відношення
називається кутовим збільшенням оптичної системи, а відношення
називається лінійним збільшенням оптичної системи.
Література.
1.Боровий В.О. Автоколімаційні, поляризаційні і лазерні вимірювання в геодезії: Монографія. Чернігів, РВВ- ЧДІЕіУ- НЦ МДВУ, 1999, - 231с. 2.Кузнецов П.Н., Васютинский Н.Ю., Ямбаев Х.К. Геодезическое инструментоведе- ние: Учебник для вузов. – М.: Недра, 1984, - 364с. 3.Островский А.Л., Маслюч Д.И., Гребенюк В.Г. Геодезическое прибороведение. Львов. Вища школа, 1983.- 205с. 4.Костецька Я.М. Геодезичні прилади. Частина ІІ. Електронні геодезичні прилади: Підручник для студентів геодезичних спеціальностей вузів. – Львів: ІЗМН, 2000- 324 с. 5.Літнарович Р.М. Польовий компаратор ЧДІЕіУ. Чернігів, ЧДІЕіУ, 2002, - 16 с. 6.Літнарович Р.М., Мардієва Л.П., Ярош Ю.В. Будова і робота світловіддалеміра СТ5. Навчальний практикум по курсу “Електронні геодезичні прилади”, ЧДІЕіУ,Чернігів,2000, - 38 с.
ЧЕРНІГІВСЬКИЙ ДЕРЖАВНИЙ ІНСТИТУТ ЕКОНОМІКИ І УПРАВЛІННЯ
ГЕОДЕЗИЧНІ ПРИЛАДИ
КОНСПЕКТ ЛЕКЦІЙ
Для студентів спеціальностей 6.07 09 04 “Землевпорядкування та кадастр” 7.07 09 08 “Геоінформаційні системи і технології” Автори: Боровий Валентин Олександрович, доктор технічних наук, професор; Літнарович Руслан Миколайович, кандидат технічних наук, доцент Комп’ютерний набір у видавничому редакторі Word (Пакет Office XP) for Windows, редагування та макетування: Комов К.С. Кафедра геоінформатики і геодезії м. Чернігів вул. Стрілецька,1 URL:www.geci.cn.ua E-mail:rector@geci.cn.ua Тел.: (0462) 179-308 (04622) 5-61-70
|

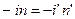 (2.15)
(2.15)
 (2.16)
(2.16) (2.17)
(2.17)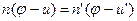 (2.18)
(2.18)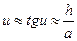 ,
, 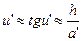 ,
, 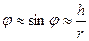 (2.19)
(2.19)
 (2.20)
(2.20)
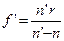 , (2.21)
, (2.21)
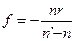 (2.22)
(2.22)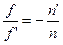 , (2.23)
, (2.23) (2.24)
(2.24) (2.25)
(2.25)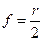 (2.26)
(2.26)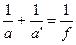 (2.27)
(2.27)
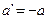 (2.28)
(2.28)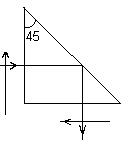

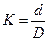 (2.29)
(2.29) (2.30)
(2.30)
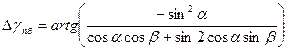 (2.31)
(2.31) (2.32)
(2.32)
 (2.33)
(2.33)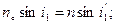
 (2.34)
(2.34)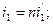
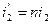 (2.35)
(2.35) (2.36)
(2.36) вираз(2.36) остаточно запишемо у вигляді:
вираз(2.36) остаточно запишемо у вигляді: (2.37)
(2.37)
 - називається оптичною силою лінзи. За одиницю вимірювання оптичної сили приймається діоптрія, що відповідає оптичній силі лінзи з фокусною відстанню 1 мм. Оптична сила збиральної лінзи позитивна, а розсіюючої – негативна. Для тонкої лінзи
- називається оптичною силою лінзи. За одиницю вимірювання оптичної сили приймається діоптрія, що відповідає оптичній силі лінзи з фокусною відстанню 1 мм. Оптична сила збиральної лінзи позитивна, а розсіюючої – негативна. Для тонкої лінзи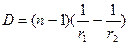 (2.38)
(2.38) (2.39)
(2.39)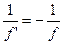 (2.40)
(2.40) (2.41)
(2.41) (2.42)
(2.42)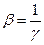 (2.43)
(2.43) (2.44)
(2.44) (2.45)
(2.45)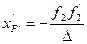 (2.46)
(2.46)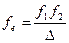 (2.47)
(2.47) (2.48)
(2.48) (2.49)
(2.49)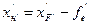 (2.50)
(2.50)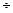 (2.48), будемо мати
(2.48), будемо мати (2.51)
(2.51) (2.52)
(2.52)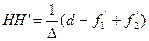 (2.53)
(2.53)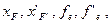 (2.54)
(2.54) (2.55)
(2.55) (2.56)
(2.56)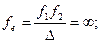
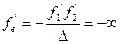 (2.57)
(2.57)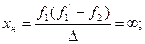
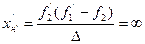 (2.58)
(2.58)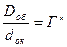 (2.59)
(2.59)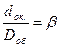 (2.60)
(2.60) Рис.10.11 Телескопічна система
Рис.10.11 Телескопічна система


