Линейная зависимость и независимость векторовНабор векторов Базис R2.и R3 d={α,β}=[ α ]εR^2 [β] d={α,β,γ}=[ α ]εR^3 [β] [γ] Разложение произвольного вектора по базису. Каждый вектор на плоскости может единым образом представлен в линейной комбинации базисных векторов на этой плоскости(этого пространства).Коэффициент этой линейной комбинации называется координатой вектора в данном базисе. Замечание. 2 коллинеарные векторы зависимы. 3 коллинеарные векторы в пространстве также линейно зависимы если векторы не коллинеарные, то они образуют базис на плоскости, а не коллинеарные базис в пространстве.
|
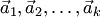называется системой векторов. Система из 
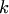векторов 
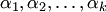, не все равные нулю одновременно, что 
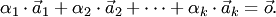Система из 
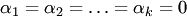, т.е. когда линейная комбинация в левой части равенства тривиальная. 1. Один вектор 
тоже образует систему: при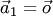 
— линейно зависимую, а при 
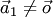— линейно независимую. 2. Любая часть системы векторов называется подсистемой. Базисом в трехмерном пространстве R3 называется упорядоченная тройка любых линейно-независимых векторов.
