Определение, условие существования и вычисление обратной матрицы.Матрица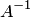 
называется обратной для квадратной матрицы А, если
где Е – единичная матрица того же порядка, что и А.
Матрицу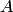 
называют обратимой, если для нее существует обратная, в противном случае — необратимой.. Если определитель матрицы 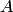равен нулю 
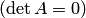, то для нее не существуетобратной.Найти обратную матрицу для 
. 1. Вычислить определитель.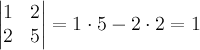 
. Определитель не равен нулю, поэтому обратная матрица существует 2. Вычислить алгебраические дополнения для каждого элемента. Алгебраическое дополнение для левого верхнего элемента (для 1). Он стоит в первой строке и первом столбце. Мысленно вычеркнем их. Останется 5. Поэтому алгебраическое дополнение 
.Алгебраическое дополнение для 2 (1-я строка, 2-й столбец): 
.
Алгебраическое дополнение для 2 (2-я строка, 1-й столбец): 
.Алгебраическое дополнение для 5 (2-я строка, 2-й столбец):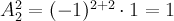 
. 3. Составить матрицу из алгебраических дополнений. 
. 4. Транспонировать матрицу 
из шага 3.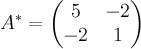 
. 5. Умножить матрицу 
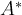на число, обратное определителю. Определитель у нас был равен 1. 
.
