Метод рационализации при интегрировании простейших иррациональных функций.
Интегралы типа тельные числа, причем c 2 + d 2 ≠ 0, сводятся к интегралам от ра- циональной функции путем подстановки (заменой переменной):
Тогда
где v=HOK{ n1 …nk }– наименьшее общее кратное знаменате- лей дробей
В частности, интегралы вида ∫ R (x; тегральная функция R (x; своих аргументов, рационализуются заменой переменной x = tv, dx =ν tv-1 dt, где ν = НОК{ k,..., m }.
|
dx, где m1,..., m k – целые; n1,..., n k – натуральные; a, b, c, d – действи-
и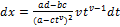 
,
.
;...; 
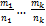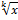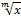) dx, где подын-
