Действия над матрицами. Суммой (разностью)C= A+ B(C= A− B) двух матриц называется такая матрица , элементы которой равны сумме (разности) соответствующих элементов матриц A и
Суммой (разностью) C= A+ B(C= A− B) двух матриц Произведением матрицы Произведением матрицы A размера m×s на матрицу B размера s×nназывается матрица C размера m×n, элементы которойравны cij= ai1b1j + ai2b2j + … + aisbsj, т. е. чтобы получить cij, нужно элементы i-й строки A умножить на соответствующие элементыj-го столбца B и полученные произведения сложить. Согласно этому определению, произведение матриц существует, если число столбцов первой из них равно числу строк второй. Например,C= Элемент c11 получаем, умножив элементы первой строки матрицы A на соответствующие элементы первого столбца матрицы Bи сложив эти произведения, т. е. c11= 3 ⋅(−1) + 2 ⋅2 = −3 + 4 =1. Аналогично C12= 3 ⋅3 + 2 ⋅(−2) = 5; c13= 3⋅1+ 2 ⋅5 =13; c21=1⋅(−1) + 4 ⋅2 = 7; c22= =1⋅3 + 4 ⋅(−2) = −5; c23=1⋅1+ 4 ⋅5 = 21. Из определения произведения матриц следует, что не всякиематрицы можно перемножить. Например, произведение
|

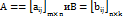 называется такая матрица
называется такая матрица 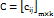 , элементы которой равны сумме (разности) соответствующих элементов матриц A и B, т. е.
, элементы которой равны сумме (разности) соответствующих элементов матриц A и B, т. е. 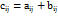 (
(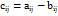 ), i= 1, m, j= 1, n. Отметим, что складываются матрицы одинаковых размеров.
), i= 1, m, j= 1, n. Отметим, что складываются матрицы одинаковых размеров.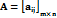 на число λ (или числа λна матрицу A) называется матрица
на число λ (или числа λна матрицу A) называется матрица 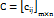 , элементы которойравны соответствующим элементам матрицы A, умноженным на λ,т. е. cij= λ⋅aij, i=1, m, j=1, n. Записывают C = λ ⋅A или C = A⋅ λ. Операции сложения, вычитания и умножения на число называют линейными операциями над матрицами. Выражение αA + βBназывается линейной комбинацией матриц A и B.
, элементы которойравны соответствующим элементам матрицы A, умноженным на λ,т. е. cij= λ⋅aij, i=1, m, j=1, n. Записывают C = λ ⋅A или C = A⋅ λ. Операции сложения, вычитания и умножения на число называют линейными операциями над матрицами. Выражение αA + βBназывается линейной комбинацией матриц A и B.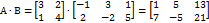
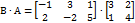 не существует, т. к. строка матрицы B2x3содержит 3 элемента, астолбец матрицы A2x2только 2 элемента. Для квадратных матриц одного порядка оба произведенияA⋅B и B ⋅A существуют, но в общем случае A⋅B ≠ B ⋅A. Например,
не существует, т. к. строка матрицы B2x3содержит 3 элемента, астолбец матрицы A2x2только 2 элемента. Для квадратных матриц одного порядка оба произведенияA⋅B и B ⋅A существуют, но в общем случае A⋅B ≠ B ⋅A. Например,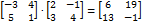 , а
, а 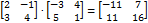 .
.


