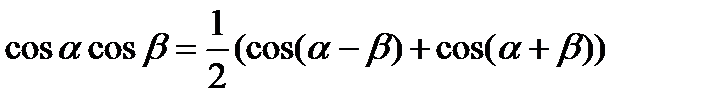Интегрирование функции рационально зависящих от тригонометрических.
Рациональной функцией R (u;v ) 2-х переменных u и v называет отношение
Если функция R(sinx;cosx) нечетна относительно sinx, т.е. R(-u;v)=-R(u;v), то подстановка cosx=t; Если функция R(sinx;cosx) нечетна относительно cosx, т.е .R(u;-v)=-R(u;v), то подстановка sinx=t; Если функция R(sinx;cosx) удовлетворяет свойству R(-u;-v)=-R(u;v), то применима подстановка tgx=t, при этом
|
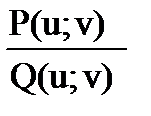многочленов P(u;v) и Q(u;v) двух переменных u и v
, 
, 
, 
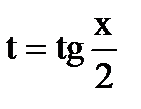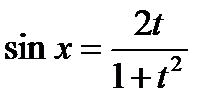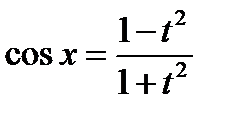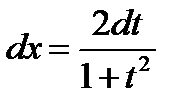.(универсальная тригонометрическая подстановка)
, 
, 
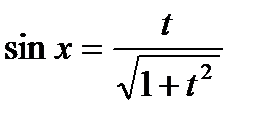. Для интегралов вида 
, где m и n – целые числа, используются след. Приемы:1) подстановка sin x = t, если n – нечетное число; 1) подстановка cosx= t, если m – нечетное число;3) формулы 
, 
, 
, если m и n –четные числа;4)Подстановка tgx=t,если m+n – отрицательное четное число. 
