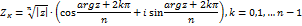Действия над комплексными числами в тригонометрической форме
Z1 = r1(cosf1+ isinf1) Z2 = r2(cosf2+ isinf2) Z1*Z2 = r1(cosf1 + isinf1) * r2(cosf2+ isinf2) = r1*r2[(cosf1*cosf2- sinf1*sinf2) + (cosf1*sinf2+ sinf1*cosf2)i] = = r1*r2[cos(f1+ f2) + sin(f1+ f2)i] Z1/Z2 = [r1(cosf1+ isinf1)] / [r2(cosf2+ isinf2)] = (r1/r2) * [(cosf1+ isinf1) * (cosf2- isinf2) / (cos2f2+ isin2f2)] = = (r1/r2) * [cos(f1- f2) + sin(f1- f2)i] Zn = rn(cosfn + isinfn) Z1/n= r1/n[cos((f + 2*pi*k)/n) + isin((f + 2*pi*k)/n)], k = 0, 1,..., n-1 Извлечение корня n–степени из комплексного числа определяем, как действие,обратное возведению
Показательная форма комплексного числа
Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа: z=r где Отсюда вытекают следующие широко используемые равенства:
|
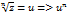=z, или 
= 
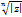- арифметический корень argu= 
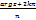,к=0,1
= 
,
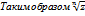