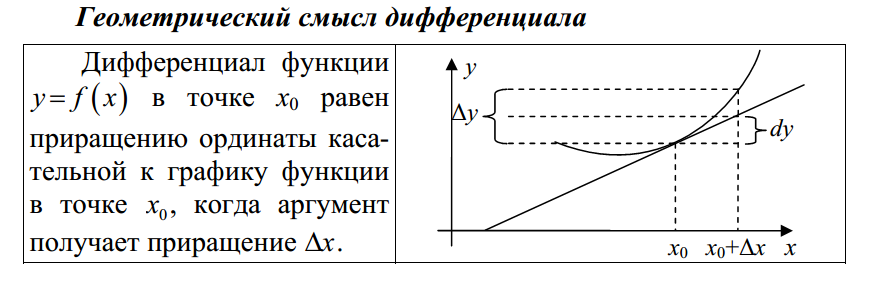
Дифф.функции.Геометрический смысл производной и дифференциал.
22.Инвариантность формы первого дифференциала. Дифференциалы высшего порядка. Инвариантность формы первого дифференциала: Дифферинциал функции z=g(y) в точке y0 имеет вид:dz=g’(y0)dy,где dy -дифференциал тождественного отображения yày0:dy(h)=h, h Дифференциалы высших порядков: Дифференциалом порядка n, где n > 1, от функции
|
R.Пусть теперь y=f(x), x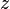 
в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть 
