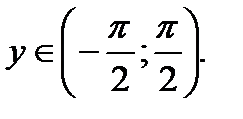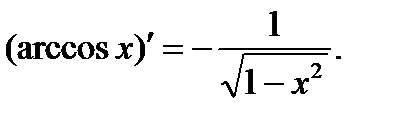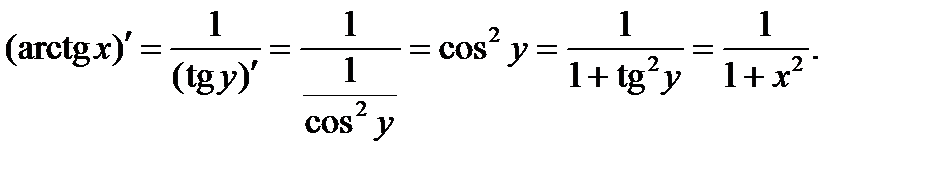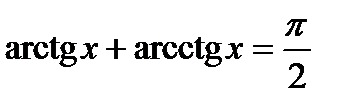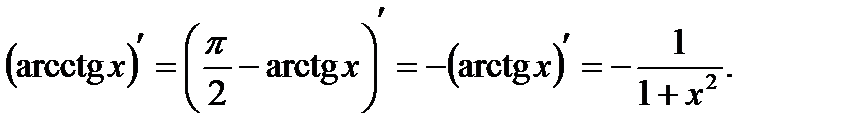Производные основных элементарных функций.
Производные_основных элементарных функцийСтепенная_функция Дадим аргументу x приращение ∆ х. Функция
Тогда Находим предел составленного отношения при ∆х→0:
Показательная_функция Найдем сначала производную функции
Итак, Теперь рассмотрим функцию
Логарифмическаяфункция Найдем производную функции Для_нее Переходя к пределу при ∆х → 0 и воспользовавшись эквивалентностью
Теперь рассмотрим функцию Таким_образом, Тригонометрические функции y = sinx, y = cosx, y = tgx, y= ctgx Для функции y = sinx имеем:
y = cosx:
Обратныетригонометрическиефункцииy = arcsinx, y = arccosx, y = arctgx, y= arcctgx Пусть y = arcsinx. Обратная ей функция имеет вид х = sin у, По правилу дифференцирования обратных функций Аналогично получаем, что y = arctgx является обратной к функции х = tg у, где
y = arcсtgx: Функции arctgx и arctgx связаны отношением
|

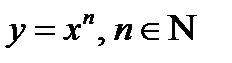
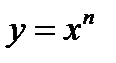 получит приращение
получит приращение 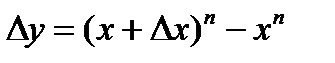 . По формуле бинома Ньютона имеем:
. По формуле бинома Ньютона имеем: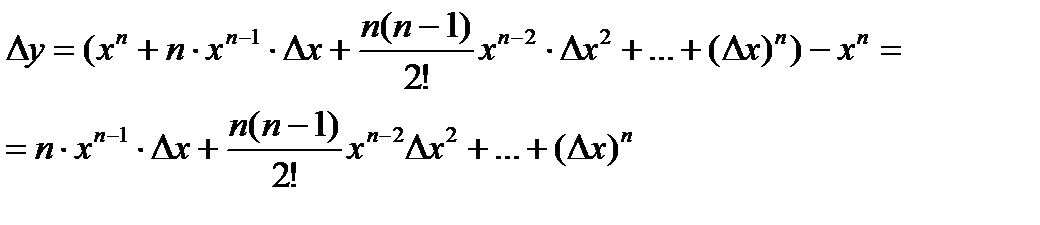


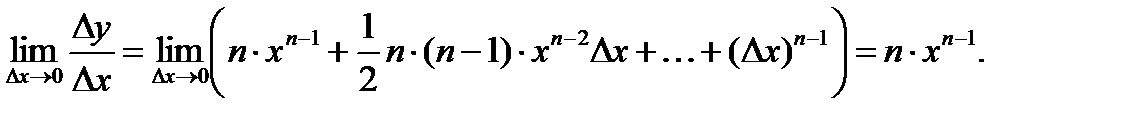 Таким образом,
Таким образом, 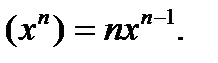
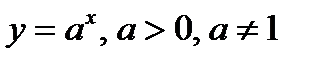
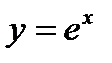 . Придав аргументу х приращение ∆х, находим приращение функции ∆у:
. Придав аргументу х приращение ∆х, находим приращение функции ∆у: 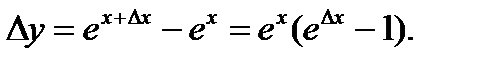
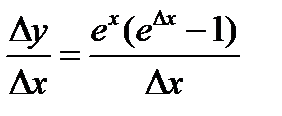 и
и 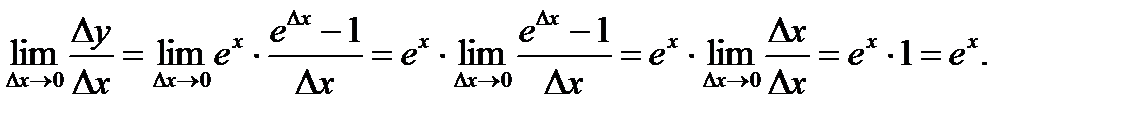 При вычислении предела воспользовались эквивалентностью
При вычислении предела воспользовались эквивалентностью 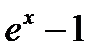 ~ х при х → 0.
~ х при х → 0.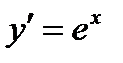 , т.е.
, т.е. 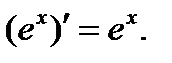
 Так_как
Так_как 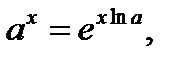 то по формуле производной сложной функции находим:
то по формуле производной сложной функции находим: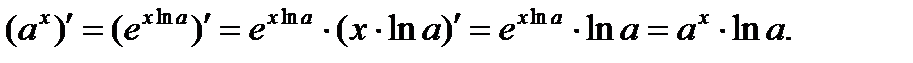 Таким образом,
Таким образом, 
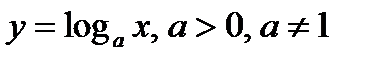
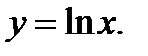
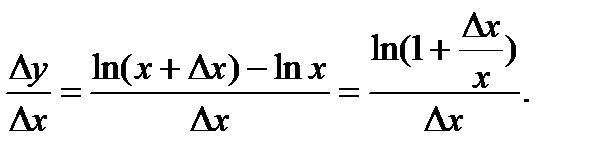
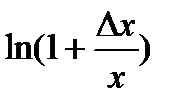 ~
~ 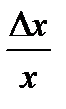 при ∆х → 0, получаем:
при ∆х → 0, получаем: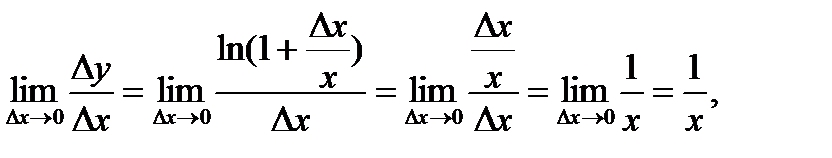 т.е.
т.е. 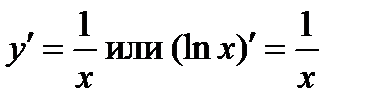 .
.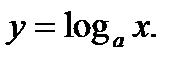 Так как
Так как 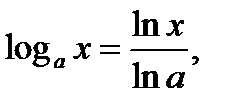 то
то 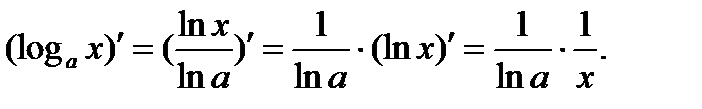
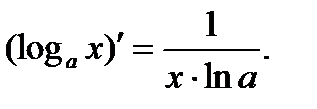
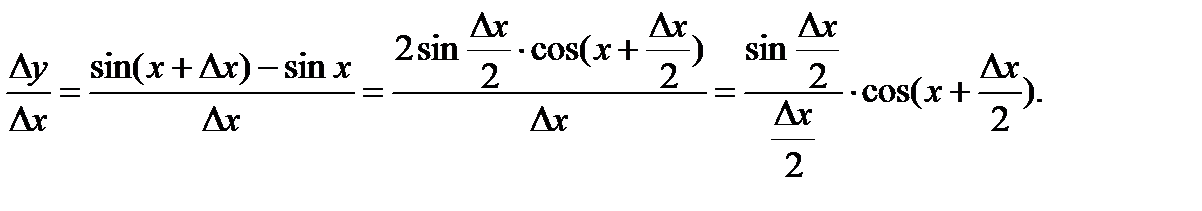 Переходя к пределу при ∆х → 0 и воспользовавшись первым замечательным пределом
Переходя к пределу при ∆х → 0 и воспользовавшись первым замечательным пределом 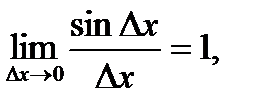 получаем
получаем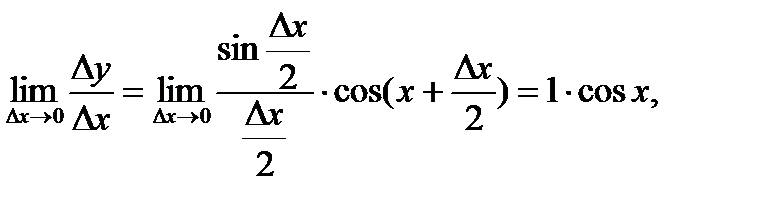 т.е.
т.е. 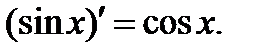
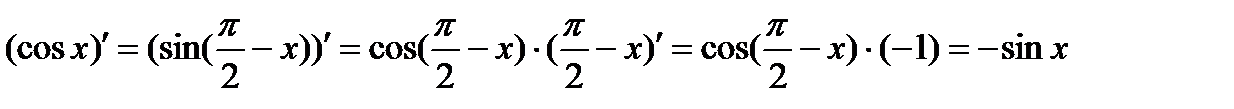 .y = tgx:
.y = tgx: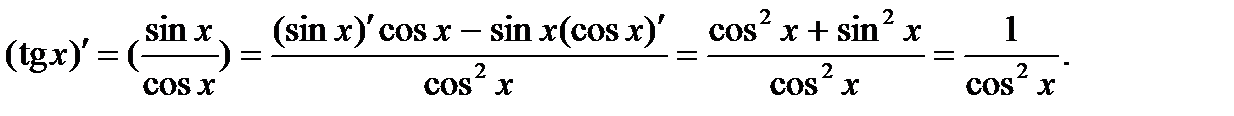 y = ctgx:
y = ctgx: 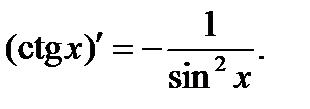
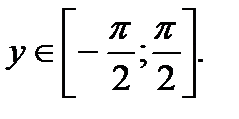 На интервале
На интервале 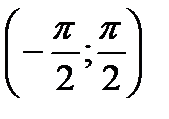 верно равенство
верно равенство 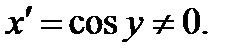
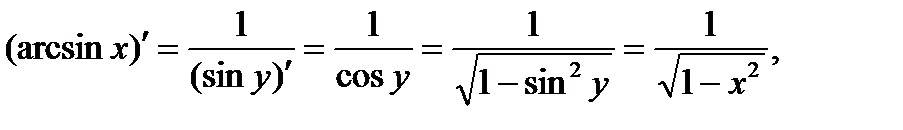 где перед корнем взят знак плюс, так как cosy> 0 при
где перед корнем взят знак плюс, так как cosy> 0 при