Ф-ция f(x)- выпуклая (вогнутая) на (a;b),если любая дуга ее графика(принадлежащая интервалу) расположена не выше (не ниже) стягивающей дугу хорды. Дифференцируемая ф-ция выпукла(вогнута) га интервале, если ее график расположен не выше(не ниже) любой касательной к нему.
Достаточные условия выпуклости и вогнутости ф-ции: если 2-ая производная 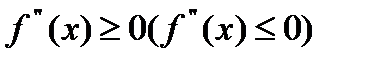 во всех точкаъ интервала (a;b), то ф-ция y=f(x) выпукла(вогнута) на этом интервале. Если неравенства строгие, то и выпуклость(вогнутость) будет строгая.
во всех точкаъ интервала (a;b), то ф-ция y=f(x) выпукла(вогнута) на этом интервале. Если неравенства строгие, то и выпуклость(вогнутость) будет строгая.
Точки перегиба - точки непрерывности ф-ции, в которых вогнутость меняется на выпуклость или наоборот. Если  -точка перегиба ф-ции, то точка (
-точка перегиба ф-ции, то точка ( )- точка перегиба этой ф-ции. В окрестности точки перегиба график диф. ф-ции лежит по разные стороны касательной к графику в точке перегиба. Достаточные условия существования точек перегиба: если вторая производная при переходе через точку
)- точка перегиба этой ф-ции. В окрестности точки перегиба график диф. ф-ции лежит по разные стороны касательной к графику в точке перегиба. Достаточные условия существования точек перегиба: если вторая производная при переходе через точку  , в которой она равна нулю или не существует, меняет знак и ф-ция непрерывна в точке
, в которой она равна нулю или не существует, меняет знак и ф-ция непрерывна в точке  , то эта точка-точка перегиба функции, а точка M
, то эта точка-точка перегиба функции, а точка M  –точка перегиба графика ф-ции.
–точка перегиба графика ф-ции.

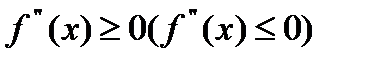 во всех точкаъ интервала (a;b), то ф-ция y=f(x) выпукла(вогнута) на этом интервале. Если неравенства строгие, то и выпуклость(вогнутость) будет строгая.
во всех точкаъ интервала (a;b), то ф-ция y=f(x) выпукла(вогнута) на этом интервале. Если неравенства строгие, то и выпуклость(вогнутость) будет строгая. -точка перегиба ф-ции, то точка (
-точка перегиба ф-ции, то точка ( )- точка перегиба этой ф-ции. В окрестности точки перегиба график диф. ф-ции лежит по разные стороны касательной к графику в точке перегиба. Достаточные условия существования точек перегиба: если вторая производная при переходе через точку
)- точка перегиба этой ф-ции. В окрестности точки перегиба график диф. ф-ции лежит по разные стороны касательной к графику в точке перегиба. Достаточные условия существования точек перегиба: если вторая производная при переходе через точку  , в которой она равна нулю или не существует, меняет знак и ф-ция непрерывна в точке
, в которой она равна нулю или не существует, меняет знак и ф-ция непрерывна в точке  , то эта точка-точка перегиба функции, а точка M
, то эта точка-точка перегиба функции, а точка M  –точка перегиба графика ф-ции.
–точка перегиба графика ф-ции.


