Комплексные числа.Определение. Комплексным числом называется число z=x+iy, где x -называется действительной частью комплексного числа и обозначается x= Re Z; y - называется мнимой частью комплексного числа и обозначается y= Im Z; i - мнимая единица.Такая запись комплексного числа называется алгебраической формой комплексного числа.Действия над комплексными числами.Сравнение a+bi=c+di означает, что a=c и b=d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части). Сложение (a+bi)+(c+di)=(a+c)+(b+d)i. Вычитание (a+bi)-(c+di)=(a-c)+(b-d)i. Умножение (a+bi)·(c+di)=ac+bci+adi+bdi2=(ac-bd)+(bc+ad)i Деление
В частности,
Формы записей1.Алгебраическая форма Запись комплексного числа z в виде x+iy, где x и y тригонометрической форме z=r(cosφ+isinφ) 3.Показательная форма z=reiφ Формула Муавра zn=
|
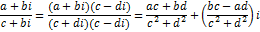
R, называется алгебраической формой комплексного числа. 2.Тригонометрическая форма
, где r-модуль, а φ-аргумент комплексного числа
