Понятие о функции комплексной переменной.
Определение: если А – некоторое множество комплексных чисел z (геометрически – множество точек комплексной плоскости), и каждому числу z При этом точка w0 = f (z0) называется образом точки z0, а z0– прообразом точки w0. В частности, если А расположено на действительной оси ох, то z = х является действительным переменным. Если же все значения w также действительны, то приходим к понятию функции действительного переменного как частному случаю функции комплексного переменного. В общем случае z = х + i у, w = u (х, у) + i v (х, у). Геометрически функцию f (z) можно рассматривать как отображение множества А на множество В, переводящее точку (х, у) множества А в точку (u, v) множества В. Высказывание “ функция w = f (z) определена на множестве А” эквивалентно следующему: “ каждой точке (х, у) из А поставлены в соответствие действительные числа u и v ”. Иными словами, на множестве А определены две действительные функции
Например, соотношение w = z2 = (x +iy)2 = x2 – y2 + i2xy эквивалентно следующим: u = x2 – y2, v = 2xy.
|

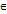 А поставлено в соответствие по некоторому закону число w
А поставлено в соответствие по некоторому закону число w  двух действительных переменных х и у. Итак, задание функции комплексного переменного w = f (z) равносильно заданию двух функций двух действительных переменных
двух действительных переменных х и у. Итак, задание функции комплексного переменного w = f (z) равносильно заданию двух функций двух действительных переменных 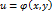 и u=
и u= 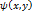 .
.


